K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

3 tháng 4 2023
AB=BM
nên \(S_{QAB}=S_{QBM}\)
DA=AQ
=>\(S_{BDA}=S_{BAQ}\)
=>\(S_{QAM}=2\cdot S_{ABD}\)
Tương tự, ta được: \(S_{MBN}=2\cdot S_{ABC};S_{NCP}=2\cdot S_{BCD};S_{PDQ}=2\cdot S_{ADC}\)
=>\(S_{MNPQ}=5\cdot S_{ABCD}=300\left(cm^2\right)\)

BT
15 tháng 6 2021
Cho hình thang ABCD có diện tích = 60m2, kéo dài BC 1 đoạn BE= ab, kéo dài BC 1 đoạn CG= BC, kéo dài Cd 1 đoạn Dh = CD. kéo dài DA 1 đoạn AK= AD. Tính diện tchs hình tứ giác ABCD
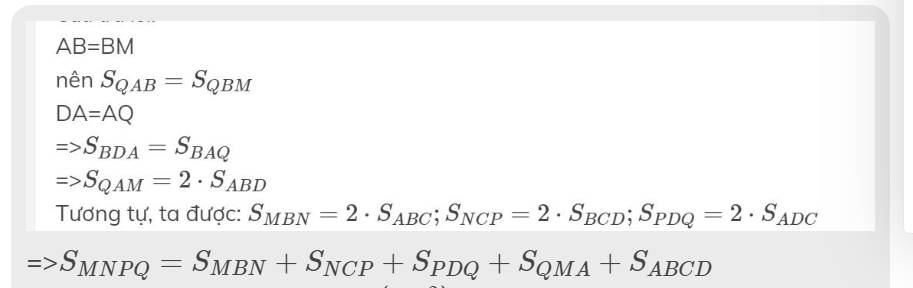

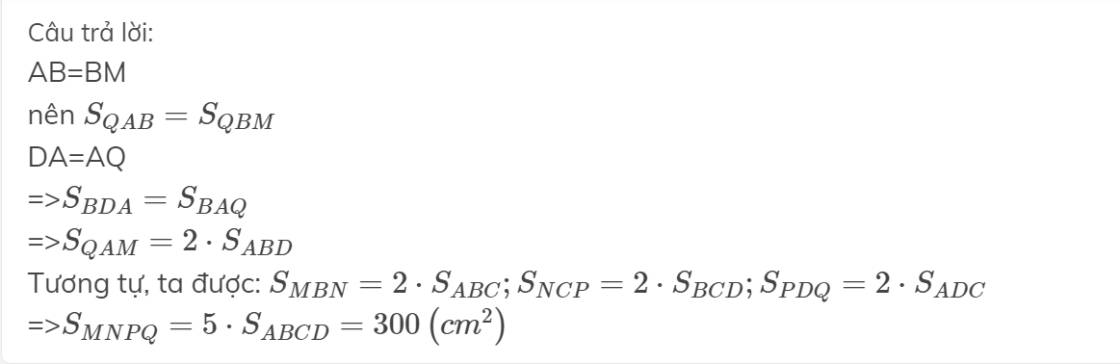
Nối M với C; N với D; P với A và Q với B
Nối A với C; B với D
Ta có S(ABCD)=S(ABD)+S(BCD)=S(ABC)+S(ACD)
Xét tg ABQ và tg ABD có chung đường cao hạ từ B xuống DQ và cạnh đáy AQ=AD nên S(ABQ)=S(ABD)
Xét tg ABQ và tg BMQ có chung đường cao hạ từ Q xuống AM và cạnh đáy AB=BM nên S(ABQ)=S(BMQ)
=> S(ABQ)=S(BMQ)=S(ABD) => S(AMQ)=S(ABQ)+S(BMQ)=2xS(ABD) (1)
Chứng minh tương tự khi xét các tam giác BCD với tg CDN và tg CDN với tg DNQ => S(CNP)=2xS(BCD) (2)
Từ (1) và (2) => S(AMQ)+S(CNP)=2xS(ABD)+2xS(BCD)=2x[S(ABD)+S(BCD)]=2xS(ABCD)
Chứng minh tương tự ta sẽ có kết quả S(DPQ)+S(CMN)=2x[S(ACD)+S(ABC)]=2xS(ABCD)
S(MNPQ)=[S(AMQ)+S(CNP)]+[S(DPQ)+S(CMN)]+S(ABCD)=5xS(ABCD)=5x25=125 cm2
=>\(S_{MNPQ}=S_{MBN}+S_{NCP}+S_{PDQ}+S_{QMA}+S_{ABCD}\)
\(=5\cdot S_{ABCD}=5\cdot25=125\left(cm^2\right)\)