Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì BC=CD(gt)
=> ΔBDC cân tại C
=>\(\widehat{CBD}=\widehat{CDB}\)
b)Vì BD là tia phân giác của \(\widehat{CBA}\)
=>\(\widehat{ABD}=\widehat{CBD}\)
Mà \(\widehat{CBD}=\widehat{CDB}\left(cmt\right)\)
=>\(\widehat{ABD}=\widehat{CDB}\) . Mà hai góc này ở vị trí soletrong
=>AB//DC
=>ABCD là hình thang

Xét ▲ADC và ▲BCD có:
AD = BC ( gt )
AC = BD ( gt )
DC chung
=> ▲ADC = ▲BCD ( c.c.c )
=> góc D = góc C ( c.t.ứ )
cmtt ta đc góc A = Góc B
Mà Góc D + góc A + Góc C + Góc B=360o
=> 2GócA+2GócD=360o
-> gócA+gócD=180o ( 2 góc trong cùng phía )=>AB//DC -> ABCD là hình thang
Vì góc D = góc C (cmt) nên ABCD là hình thang cân

a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân

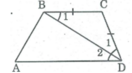
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.
⇒ ∠ B 1 = ∠ D 1 (tính chất tam giác cân)
Mà ∠ D 1 = ∠ D 2 ( Vì DB là tia phân giác của góc D)
Suy ra: ∠ B 1 = ∠ D 2
Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)
Vậy ABCD là hình thang.


ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang
Học tốt
\(DB\)là phân giác \(\widehat{ADC}\)suy ra \(\widehat{ADB}=\widehat{CDB}\)(1)
\(BC=CD\)suy ra \(\Delta CBD\)cân tại \(C\)suy ra \(\widehat{CBD}=\widehat{CDB}\)(2)
(1)(2) suy ra \(\widehat{ADB}=\widehat{CBD}\)
mà hai góc này ở vị trí so le trong suy ra \(BC//AD\).
Suy ra \(ABCD\)là hình thang.