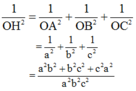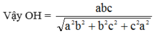Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
Ta có: 
Diện tích tam giác OAB là: 
Thể tích khối chóp O.ABC là:
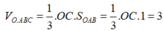
Chọn A.
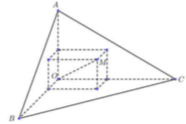
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó 
Hay 
Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có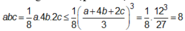 
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 8( c m 3 ) khi a = 4b = 2c
Đáp án D
Từ giả thiết ta thấy 
và OBC là tam giác vuông nên thể tích cần tìm là:
VO.ABC = 1 3 OA.SOBC = 1 6 OA.OB.OC = abc 6
Chọn A.
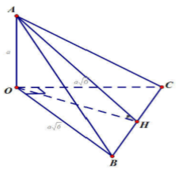
Ta có: 
Trong (OBC) kẻ OH ⊥ BC tại H thì có ngay BC ⊥ (OAH)
Có 
Do đó: 
(vì ∆ OHA vuông tại O nên A H O ^ < 90 ° )
Ta có: 
∆
OHA vuông tại O nên 
Vậy góc giữa hai mặt phẳng ((ABC),(OBC)) bằng 30 °
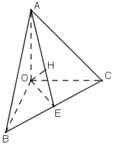
- Tam giác OBC vuông ở O và có đường cao OE nên:
1 O E 2 = 1 O B 2 + 1 O C 2 5
- Tam giác AOE vuông ở O và có đường cao OH nên:
1 O H = 1 O A 2 + 1 O E 2
Từ (5) và (6) suy ra
