Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
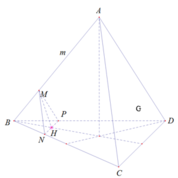
Trong (ABC) kẻ MN // AC ( N ∈ BC)
Trong (ABD) kẻ MP // AD ( P ∈ BD)
⇒ (MNP) là mặt phẳng cần tìm
Xét tam giác MNP có MN = MP =NP (= a - m )
⇒ tam giác MNP đều
Mà NP // CD và BG là trung tuyến tam giác BCD
⇒ BG cắt NP tại H là trung điểm NP
⇒ MH là đường cao tam giác MNP
Ta có: PH = a - m 2 và MP = a – m. Áp dụng định lý pitago, ta có: MH = 3 2 a - m
Và NP = a – m
SMNP = MH . NP 2 = 3 4 a - m 2

Đáp án A
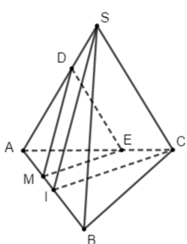
Qua M kẻ đường thẳng song song với IC cắt AC tại E và kẻ đường thẳng song song với SI cắt SA tại D.
Khi đó thiết diện của mặt phẳng với tứ diện là tam giác MED
Lại có: MD // SI ⇒ A M A I = M D S I
ME // IC ⇒ A M A I = M E I C
Do đó M D S I = M E I C
Vì S.ABC là tứ diện đều nên SI = CI (hai đường trung tuyến trong hai tam giác đều có chung cạnh)
Suy ra MD = ME
Vậy tam giác MED cân tại M.
Đáp án B

Đáp án B
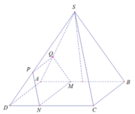
Trong mặt phẳng (ABCD) kẻ Mx song song với BC
Mx cắt CD tại N
⇒ MN // (SBC) (1)
Trong mặt phẳng (SCD) kẻ Ny song song với SC
Ny cắt SD tại P
⇒ NP // (SBC) (2)
Trong mặt phẳng (SAB) kẻ Mz song song với SB
Mz cắt SA tại Q
⇒ MQ // (SBC) (3)
Từ (1), (2), (3), ta có thiết diện MNPQ tạo bởi mặt phẳng (P) và hình chóp SABCD
Xét tứ diện MNPQ có:
A M A B = D N D C = A Q A S = D P D S
⇒ PQ // AD ⇒ PQ // MN
⇒ MNPQ là hình thang

Đáp án C
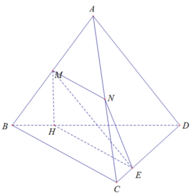
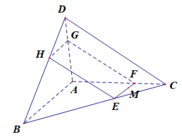
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang

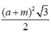


Đáp án B
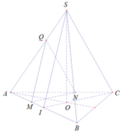
Trong (ABC), kẻ đường thẳng d đi qua M song song CI
d cắt AC tại H
Trong (SAB) kẻ đường thẳng x đi qua M và song song SI
X cắt SA tại J
⇒ (MHJ) là thiết diện cần tìm
Gọi tứ diện đều cạnh 2a ⇒ AI = a
Ta có AM = x và M J S I = A M A I (MJ // SI theo cách dựng)
A M A I = M H C I (MH // CI theo cách dựng)
J H S C = A H A C = A M A I
⇒ MJ = x a . 3 a = x 3
MH = x a . 3 a = x 3
JH = x a . 2 a = 2x
Chu vi thiết diện MHJ là: x 3 + x 3 + 2x = 2x ( 3 + 1 )