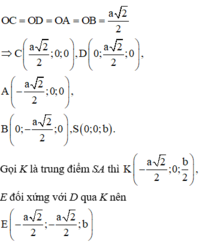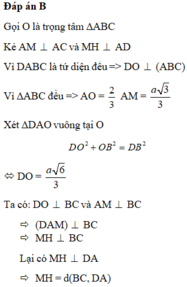
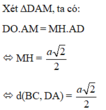
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

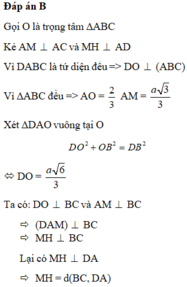
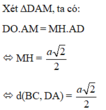


Đáp án B.
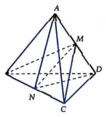
Gọi M,N lần lượt là trung điểm của AD và BC. Ta có ∆ A B D và ∆ A C D đều cạnh bằng a nên B M = C M = a 3 2 ⇒ ∆ M B C cân tại M và MN là đường cao của ∆ M B C ⇒ M N ⊥ B C
Tương tự, ∆ N A D cân tại N nên NM là đường cao của ∆ N A D ⇒ N M ⊥ A D
Suy ra MN là đoạn vuông góc cung của AD và BC.
Vậy d A D ; B C = M N = B M 2 - B C 2 2 = a 3 2 2 - a 2 2 = a 2 2

Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
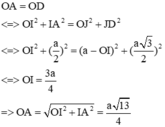
Ta có:

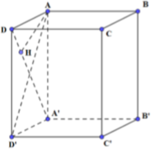
Kẻ
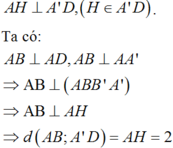
Gọi độ dài đoạn AD là x
∆ A D A ' vuông tại A,
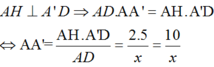
Lại có:
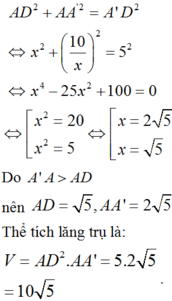
Chọn: C

Phương pháp:
- Gắn hệ tọa độ Oxyz với O là tâm hình vuông đáy,

- Xác định tọa độ các điểm cần thiết và tính khoảng cách.
Cách giải:
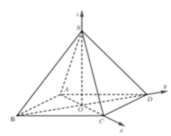
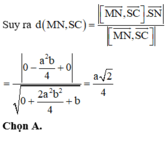
Gắn hệ trục tọa độ như hình vẽ, giả sử SO = b ta có: