K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
Hướng dẫn (khuya quá rồi).
Trong mp (ADN), lấy Q thuộc AD sao cho \(NP||GQ\)
\(\Rightarrow\left(\overrightarrow{MG};\overrightarrow{NP}\right)=\left(\overrightarrow{MG};\overrightarrow{GQ}\right)=180^0-\widehat{MGQ}\)
Áp dụng định lý hàm cos là tính được (\(GP=\dfrac{2}{3}NP\) ; tính MQ dựa vào hàm cos tam giác AMQ)

CM
24 tháng 3 2018
Đáp án C
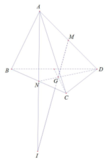
Xét (AND) có MG ∩ AN = I
Mà AN ∈ (ABC)
⇒ MG ∩ (ABC) = I
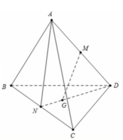

Ta có G ϵ (BCD) và (GMN) (1)
Trong (ACD) có MN và CD cắt nhau tại H
H ϵ (BCD) và (GMN) (2)
Từ (1) và (2) suy ra GH là giao tuyến của (BCD) và (GMN)
Ta có: G là điểm chung thứ nhất của (MNG) và ( BCD)
Trong (ACD): MN cắt CD=I
I là điểm chung thứ hai của (MNG) và (BCD)
Vậy (MNG) cắt (BCD)= GI