Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi I và J lần lượt là trung điểm AB,CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).
S A ⊥ A D , A B ⊥ S A D ,IJ// S A D ⇒ d IJ; S A D = d I; S A D = I A = a 2

Đáp án B
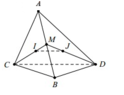
Gọi M là trung điểm của AB
Tam giác ABC có trọng tâm I suy ra M I M C = 1 3
Tam giác ABC có trọng tâm J suy ra M J M D = 1 3
Khi đó M I M C = M J M D ⇒ I J / / C D (định lí Talet)

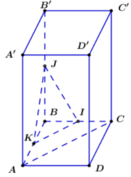
Gọi K là trung điểm của AB ⇒ IK // BC (tính chất đường trung bình của tam giác)
Chọn B.

Đáp án A.
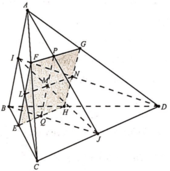
Ta có hình vẽ bên.
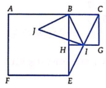
Từ A C = 3 ⇒ A B = B E = E F = F A = 2 B C = C G = G H = H B = 1 . Do I = E C ∩ G H ⇒ I là trung điểm của HG. Suy ra B I = B H 2 + H G 2 2 = 1 2 + 1 2 2 = 5 2
Q B ; - 90 ° ( I ) = J ⇒ B I ⊥ B J B I = B J ⇒ ∆ B I J vuông cân tại B.
Vậy I J = B I 2 = 5 2 . 2 = 10 2


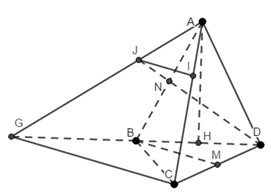





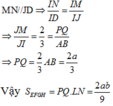
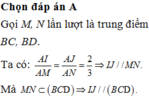
Gọi M, N lần lượt là trung điểm của BD, DC
Mà I, J lần lượt là trọng tâm các tam giác ABC, ABD nên: