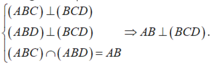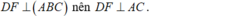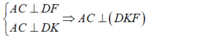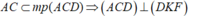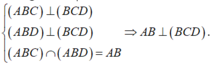Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

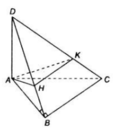
Gọi K là trung điểm CD \(\Rightarrow CD\perp\left(SIK\right)\)
\(\Rightarrow\widehat{ISK}\) là góc giữa SI và (SCD)
\(SI=\dfrac{a\sqrt{3}}{2}\) ; \(IK=a\)
\(SK=\sqrt{SI^2+IK^2}=\dfrac{a\sqrt{7}}{2}\)
\(sin\widehat{ISK}=\dfrac{IK}{SK}=\dfrac{2\sqrt{7}}{7}\)

Bạn ơi, độ dài cạnh AC bằng a hay bằng 2a nhỉ? Với lại đề thiếu dữ kiện về độ dài SA. Mình cho là AC = a nghen, nếu khác thì bạn chỉ cần sửa số lại là được hen và điền lại độ dài cạnh SA nếu đề có nhé, mình sẽ làm một cách tổng quát nhất có thể.
Bạn vẽ hình giúp mình nha!
Kẻ \(AH\perp BC\left(H\in BC\right)\), xét \(\Delta ABC\) vuông tại A có AH là đường cao ứng với cạnh huyền:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{a^2}+\dfrac{1}{a^2}\Rightarrow AH=\dfrac{a\sqrt{2}}{2}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp BC\left(SA\perp\left(ABC\right)\right)\\AH\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAH\right)\) \(\Rightarrow BC\perp SH\)
\(\Rightarrow\left(\stackrel\frown{\left(SBC\right),\left(ABC\right)}\right)=\left(\stackrel\frown{AH,SH}\right)=arctan\left(\dfrac{SA}{AH}\right)\)

Chọn A.
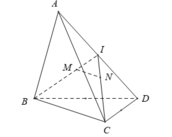
- Gọi I là trung điểm của AD.
- Do M, N là trọng tâm tam giác ABD, ACD nên:
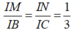
- Theo định lý Talet có: MN // BC.
- Mà: BC ⊂ (BCD), BC ⊂ (ABC).
- Vậy: MN // (BCD); MN // (ABC).