

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1.
Đáp án C là đáp án đúng
Tất cả các cạnh bên của chóp đều bằng nhau, tất cả các cạnh đáy bằng nhau, nhưng tất cả các cạnh không chắc bằng nhau (cạnh bên có thể khác cạnh đáy)
2.
\(f'\left(x\right)=\dfrac{1}{2}cos^2x-\left(\dfrac{x-1}{2}\right)sin2x\)
\(f\left(x\right)-\left(x-1\right)f'\left(x\right)=0\Leftrightarrow\dfrac{x-1}{2}cos^2x-\dfrac{x-1}{2}cos^2x+\dfrac{\left(x-1\right)^2}{2}sin2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\sin2x=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\) đáp án D
3. \(y'=\sqrt{x}+\dfrac{x}{2\sqrt{x}}=\dfrac{3}{2}\sqrt{x}\)

Chọn A.
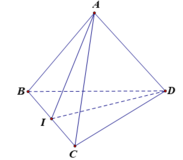
+) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao: AI ⊥ BC (1)
+) Tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao: DI ⊥ BC (2)
- Từ (1) và (2) suy ra BC ⊥ (ADI).

Đáp án A
Nếu số mặt là 6 dễ thấy số cạnh là 9, nếu số mặt là 4 thì số cạnh là 6 do đó (2) sai.

Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)