Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
B = \(\dfrac{1}{2020}+\dfrac{2}{2019}+\dfrac{3}{2018}+...+\dfrac{2019}{2}+\dfrac{2020}{1}\)
B = \(\left(\dfrac{1}{2020}+1\right)+\left(\dfrac{2}{2019}+1\right)+\left(\dfrac{3}{2018}+1\right)+...+\left(\dfrac{2019}{2}+1\right)+1\)
B = \(\dfrac{2021}{2020}+\dfrac{2021}{2019}+\dfrac{2021}{2018}+...+\dfrac{2021}{2}+1\)
B = \(2021\left(\dfrac{1}{2021}+\dfrac{1}{2020}+\dfrac{1}{2019}+...+\dfrac{1}{2}\right)\) (1)
Mà A = \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{A}{B}=\dfrac{1}{2021}\)
Ta có: \(B=\dfrac{1}{2020}+\dfrac{2}{2019}+\dfrac{3}{2018}+...+\dfrac{2019}{2}+\dfrac{2020}{1}\)
\(=\left(\dfrac{1}{2020}+1\right)+\left(\dfrac{2}{2019}+1\right)+\left(\dfrac{3}{2018}+1\right)+...+\left(\dfrac{2019}{2}+1\right)+1\)
\(=\dfrac{2021}{2020}+\dfrac{2021}{2019}+\dfrac{2021}{2018}+...+\dfrac{2021}{2}+\dfrac{2021}{2021}\)
Suy ra: \(\dfrac{A}{B}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}}{2021\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}\right)}=\dfrac{1}{2021}\)

\(A>\dfrac{2^{2018}}{2^{2018}+3^{2019}+5^{2020}}+\dfrac{3^{2019}}{2^{2018}+3^{2019}+5^{2020}}+\dfrac{5^{2020}}{5^{2020}+2^{2018}+3^{2019}}=1\)
\(B< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2019\cdot2020}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2019}-\dfrac{1}{2020}\)
=>B<1
=>A>B

Sửa đề: 2020/1+2019/2+...+1/2020
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}}{\left(1+\dfrac{2019}{2}\right)+\left(1+\dfrac{2018}{3}\right)+...+\dfrac{1}{2020}+1+1}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}}{\dfrac{2021}{2}+\dfrac{2021}{3}+...+\dfrac{2021}{2020}+\dfrac{2021}{2021}}\)
=1/2021

Lời giải:
$A=1-\frac{1}{2019}+1-\frac{1}{2020}+1-\frac{1}{2021}+1+\frac{3}{2018}$
$=4+(\frac{1}{2018}-\frac{1}{2019}+\frac{1}{2018}-\frac{1}{2020}+\frac{1}{2018}-\frac{1}{2021})$
$> 4+0+0+0+0=4$
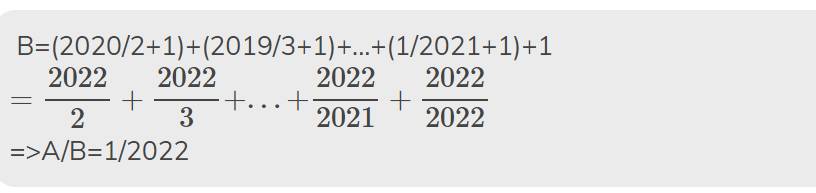
\(2T=2+\dfrac{3}{2^1}+\dfrac{4}{2^2}+...+\dfrac{2020}{2^{2018}}+\dfrac{2021}{2^{2019}}\)
\(T=2T-T=2+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2019}}-\dfrac{2021}{2^{2020}}\).
Đặt \(S=\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2019}}\Rightarrow2S=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2018}}\Rightarrow S=2S-S=1-\dfrac{1}{2^{2019}}\).
Từ đó \(T=2+1-\dfrac{1}{2^{2019}}-\dfrac{2021}{2^{2020}}< 3\).