Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TKHT có f = 15 cm
Vật sáng AB cao 4 cm đặt vuông góc với trục chính tại A.
Khoảng cách vật – tk: d= 10 cm.
a.
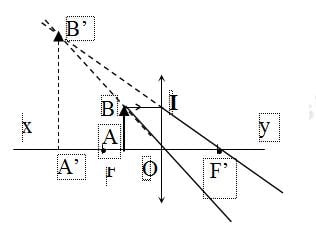
Xét tam giác OAB và tam giác OA’B’ có: góc O chung; góc A = góc A’ = 900.
Nên tam giác OAB đồng dạng với tam giác OA’B’. Ta có các tỉ số đồng dạng:
\(\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\Leftrightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\)
Xét tam giác OIF’ và tam giác F’A’B’
Có: \(\widehat{IF'O}\) = \(\widehat{B'F'A'}\)
Nên tam giác OIF’ ~ tam giác F’A’B’ . Ta có tỉ số đồng dạng:
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{F'A'}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'+OF'}\Leftrightarrow\dfrac{d}{d'}=\dfrac{f}{d'+f}\)
Thay số từ đề bài ta có:
\(\dfrac{10}{d'}=\dfrac{15}{d'+15}\Leftrightarrow10d'+150=15d'\Leftrightarrow5d'=150\)
<=> d' = 30 cm
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Leftrightarrow h'=h.\dfrac{d'}{d}=1.\dfrac{30}{10}=3\left(cm\right)\)

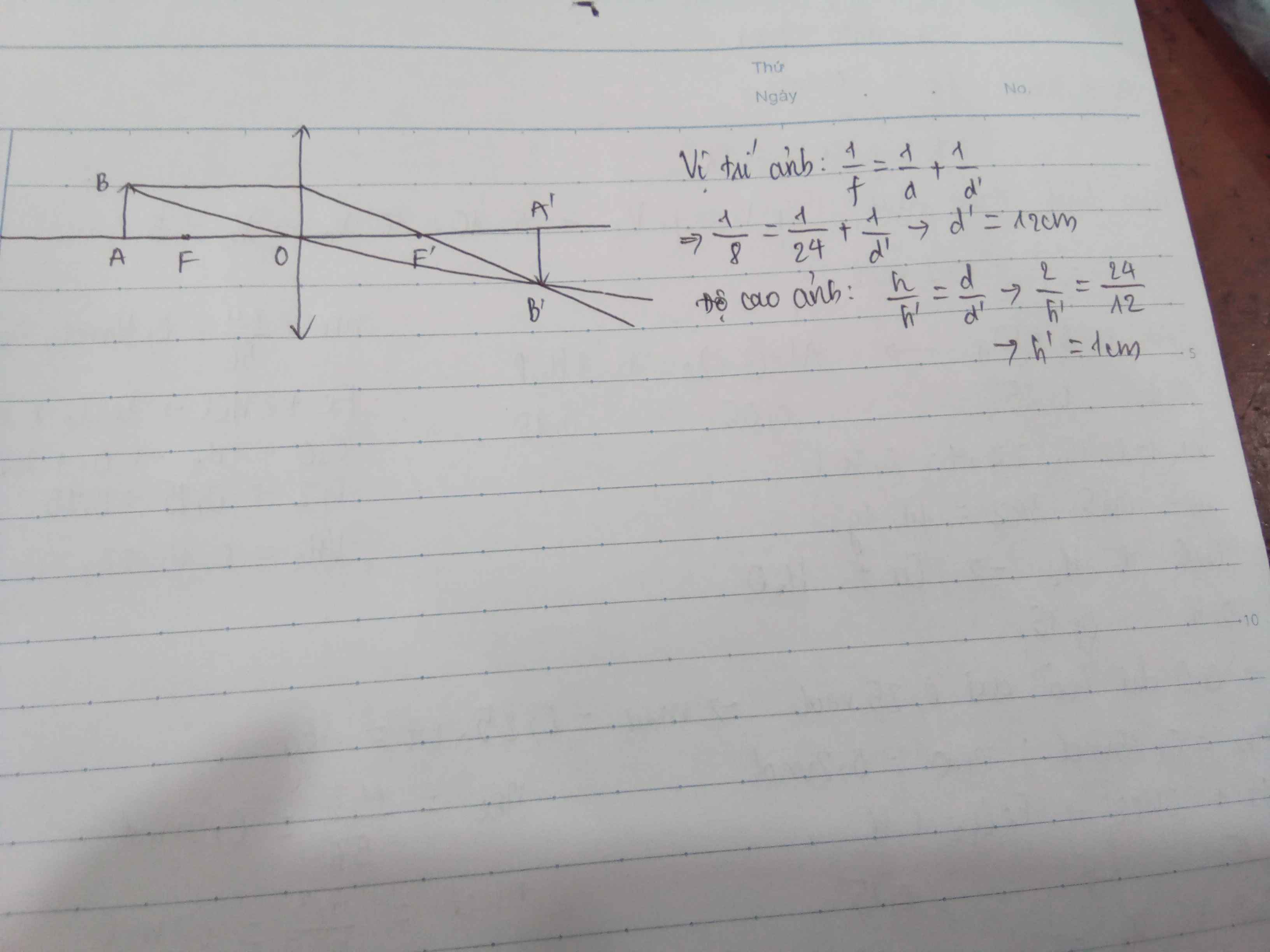
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Leftrightarrow d'=60cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{30}{60}\Rightarrow h'=4cm\)

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{9}\Rightarrow d'=\dfrac{36}{7}cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{9}{\dfrac{36}{7}}\Rightarrow h'=\dfrac{8}{7}cm\approx1,14cm\)

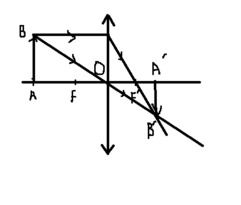
a)Ảnh A'B' là ảnh thật, ngược chiều vật và bằng vật (Hình vẽ tương đối đúng).
b)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{20}+\dfrac{1}{d'}\)
\(\Rightarrow d'=20cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{2}{h'}=\dfrac{20}{20}\Rightarrow h'=2cm\)