Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có bộ 3 số có tổng chia hết cho 3 là: {1;2;3}, {1;2;6}, {1;2;9}, {1;3;5}, {1;3;8}, {1;4;7}, {1;5;6},{1;5;9}, {1;6;8}, {1;8;9}, {2;3;4}, {2;3;7}, {2;4;6}, {2;4;9}, {2;5;8}, {2;6;7}, {2;7;9}, {3;4;5}, {3;4;8}, {3;5;7}, {3;6;9}, {3;7;8}, {4;5;6}, {4;5;9}, {4;6;8}, {5;6;7}, {6;7;8}, {7;8;9}.
Mỗi bộ số ta lập được 3! = 6 số.
Vậy có 30.6=180 số.

Chọn C
Giả sử số lập được có dạng ![]()
![]()
Ta có 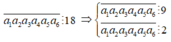
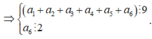
Vì ![]() nên ta có các trường hợp sau
nên ta có các trường hợp sau
Trường hợp 1:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ ![]()
+ Có 3 cách chọn chọn a 6
+ Có 5! cách chọn chọn bộ 5 số ![]()
Suy ra có 3.5! = 360 số.
Trường hợp 2:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ ![]()
+
a
6
= 0, có 5! cách chọn bộ 5 số ![]()
+
a
6
≠
0 khi đó
a
6
có 3 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ ![]()
+
a
6
= 0, có 5! cách chọn bộ 5 số ![]()
+
a
6
≠
0 khi đó
a
6
có 1 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.

Chọn A
Số phần tử của A là A 9 4 = 3024 số.
Số phần tử của không gian mẫu là n ( Ω ) = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng ![]()
Theo bài ra ta có: ![]() và
và ![]()
Suy ra ![]()
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là ![]()
Chọn 2 cặp trong 4 cặp số trên để tạo số ![]()
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48
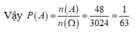

Đáp án : A
+) ![]() ; c có 4 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
; c có 4 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) ![]() ; c có 3 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
; c có 3 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) a = 7; ![]() ; b khác 9, b có 6 cách chọn.
; b khác 9, b có 6 cách chọn.
+) a = 7; c = 8; b có 6 cách chọn
Vậy có 3.4.7 + 3.3.7 + 3.6 + 6 = 171 số.

Đáp án : D
Để tính nhanh với bài này ta dùng quy tắc phần bù.
Trước tiên ta tính số các số chẵn có 5 chữ số đôi một khác nhau và được lập ra từ các chữ số của tập A.
+ Gọi các số đó là ![]()
e có 4 cách chọn( vì x là số chẵn nên e có thể là 2;34;6;8); a có 8 cách; b có 7 cách; c có 6 cách và d có 5 cách.
Nên có tất cả 4.8.7.6.5=6720 số
+ Gọi ![]() là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
Suy ra b có 3 cách chọn (b có thể là 2;4;8), a có 5 cách chọn nên có số.
+ Suy ra có tất cả 6720 - 15 = 6705 số cần tìm.

Ta cần đếm số các số tự nhiên dạng ![]() , với a;b;c là các số phân biệt thuộc tập X.
, với a;b;c là các số phân biệt thuộc tập X.
Công đoạn 1: Chọn c ∈ X, để số tự nhiên chia hết cho 5 thì chỉ có 1 cách chọn c (c = 5).
Công đoạn 2: Chọn a ∈ X\{5} , có 5 cách.
Công đoạn 3: Chọn b ∈ X\{5;a} , có 4 cách.
Vậy theo quy tắc nhân, số các số tự nhiên thỏa mãn yêu cầu là: 1.5.4 = 20 số.
Chọn C.

Số số có 3 chữ số khác nhau: \(5.5.4=100\) số
Chia tập A làm 3 tập: B={0;3}, C={1;4}, D={2;5}
Số được lập chia hết cho 3 khi 3 chữ số lấy từ 3 tập khác nhau
Do đó số số chia hết cho 3 là: \(2.2.2=8\)
Số số không chia hết cho 3: \(100-8=92\) số
Một số chia hết cho 11 khi thỏa điều kiện: Lấy chữ số đầu tiên trừ cho chữ số thứ 2 rồi cộng cho chữ số thứ 3 rồi trừ cho chữ số thứ 4… Tiếp tục quy luật này đến chữ số cuối cùng, không phân biệt kết quả là số âm hay dương. Nếu kết quả đó chia hết cho 11 thì số ban đầu sẽ chia hết cho 11Một số chia hết cho 11 khi thỏa điều kiện: Lấy chữ số đầu tiên trừ cho chữ số thứ 2 rồi cộng cho chữ số thứ 3 rồi trừ cho chữ số thứ 4… Tiếp tục quy luật này đến chữ số cuối cùng, không phân biệt kết quả là số âm hay dương. Nếu kết quả đó chia hết cho 11 thì số ban đầu sẽ chia hết cho 11
vì vậy ta có số cần tìm là n=11m nếu n có chữ số tận cung là 1 thì ta có
11m \(\equiv\)1(mod10)
\(\Leftrightarrow\)m\(\equiv\)1(mod 10)
vây m=10k+1=>n=110k+11
do n có 6 chữ số nên
10^5\(\le\)110k+11\(\le\)10^6-1
\(\dfrac{10^5-11}{110}\le k\le\dfrac{10^6-12}{110}\)
số số nguyên trong đoạn này là
\(\left[\dfrac{10^6-12}{110}\right]-\left[\dfrac{10^5-11}{110}\right]+1=9090-908+1=8183\) số chia hết cho 11 tận cùng =1
ta có 111111,.........=> số chữ số tm đề ra nhưng tận cùng =1 là 8183-...
tương tự cho tận cùng =2,=3...=9