Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số tập con của A có 8 phần tử C n 8
và số tập của A có 4 phần tử là C n 4
⇒ 26 = C n 8 C n 4 = ( n - 7 ) ( n - 5 ) ( n - 4 ) 1680
⇔ n = 20
Số tập con gồm k phần tử là C 20 k
Khi xảy ra C 20 k > C 20 k + 1
![]()
Vậy với k = 10 thì C 20 k đạt giá trị nhỏ nhất.

Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là 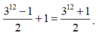
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 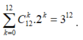
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách

Chọn B
Số tập hợp con của A khác rỗng có số phần tử là số chẵn là:
![]()
Để tính M ta xét: ![]()
![]()
Thay x = 1 ta có: ![]()
![]()
Thay x = -1 ta có: ![]()
![]()
Từ (1) và (2) ta có:
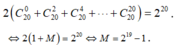

Chọn A
Lời giải.
Số tập hợp con khác rỗng có số phần từ chẵn là số cách chọn số phần tử chẵn từ 20 phần tử
Do đó số tập con là
![]()
Tính tổng trên bằng cách khai triển nhị thức Niutơn hoặc dùng máy tính cầm tay và đối chiếu các đáp án

Đáp án C
Phương pháp: Sử dụng công thức tổ hợp chập của phần tử trong khi chọn các tập hợp con có 2,4,6,…,20 phần tử.
Cách giải:
*TH1: A có 2 phần tử => có C 20 2 tập hợp con có 2 phần tử.
*TH2: A có 4 phần tử => có C 20 4 tập hợp con có 4 phần tử.
….
*TH10: A có 20 phần tử => có C 20 20 tập hợp con có 20 phần tử.
Suy ra tất cả có ∑ i = 1 10 C 20 2 i = 2 19 - 1 trường hợp.

Số tập con có hai phần tử của A là: \(C_{90}^2=4005\)
Không gian mẫu: chọn 2 tập từ 4005 tập có \(C_{4005}^2\) cách
Trung bình cộng cách phần tử trong mỗi tập bằng 30 \(\Rightarrow\) tổng 2 phần tử của mỗi tập là 60
Ta có các cặp (1;59); (2;58);...;(29;31) tổng cộng 29 cặp (đồng nghĩa 29 tập thỏa mãn)
Chọn 2 tập từ 29 tập trên có \(C_{29}^2\) cách
Xác suất: \(P=\dfrac{C_{29}^2}{C_{4005}^2}=A\)

Chọn A
Ta lấy 4 phần tử bất kì trong tập hợp gồm 9 phần tử có C 9 4 cách.
Vậy số tập con gồm 4 phần tử là C 9 4

Đáp án A.
Phương pháp: Số tập con có 2 phần tử của tập A là chỉnh hợp chập 2 của 4.
Cách giải: Số tập con có 2 phần tử của tập A là C 4 2 = 6 .