Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Theo đề bài ta có
C n 3 = 2. C n 2 ⇔ n ! 3 ! n − 3 ! = 2. n ! 2 ! n − 2 ! ⇔ 1 6 = 1 n − 2 ⇔ n = 8

Đáp án C
Nhận xét: Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng, tức là không cùng nằm trên một cạnh của tam giác ABC.
Chọn ngẫu nhiên 3 điểm từ n + 6 điểm đã cho có: C n + 6 3 (cách)
Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của tam giác ABC có: C 4 3 + C n 3 (cách)
Số tam giác lập thành là:
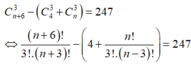
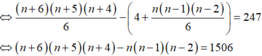
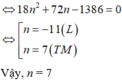

Đáp án B.
Số tam giác có 3 đỉnh là 3 trong 15 điểm đã cho bằng số cách chọn 3 điểm trong 15 điểm đã cho và bằng C 15 3 (không quan tâm đến thứ tự đỉnh).

Đáp án D.
Gọi M’ là điểm đối xứng của M qua đường thẳng d : x 1 = y − 6 − 4 ; z − 6 − 3 .
Gọi H t ; 6 − 4 t ; 6 − 3 t ∈ d là hình chiếu vuông góc của M trên d
Ta có: M H → = t ; t − 4 t ; 3 − 3 t , cho M H → . u d → = 1 + 16 t − 4 + 9 t − 9 = 0 ⇔ t = 1 2 ⇒ H 1 2 ; 4 ; 9 2
Khi đó M ' 1 ; 3 ; 6 suy ra vecto chỉ phương cuả A C → là M ' N → = 0 ; − 2 − 6 = − 2 0 ; 1 ; 3 .

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.



Chọn đáp án C.