Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
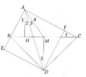

a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)

Gọi Q là điểm đối xứng với A qua M, S là điểm đối xứng với E qua M
Lấy giao điểm của DB và EC kéo dài là F, gọi G là trung điểm của OF. Nối F với I.
Dễ dàng chứng minh được: \(\Delta\)AMC=\(\Delta\)BMQ (c.g.c) => ^MAC=^MQB
Suy ra AC // BQ (2 góc so le trong bằng nhau) => ^BAC+^ABQ=1800 (1)
Ta có: ^BAC+^EAD= 2.^BAC + ^CAE + ^DAB = (^BAC+^CAE) + (^BAC+^DAB) = ^BAE+^CAD=1800 (2)
Từ (1) và (2) => ^BAC+^ABQ=^BAC+^EAD => ^ABQ=^EAD
=> \(\Delta\)ABQ=\(\Delta\)EAD (c.g.c) = >^BAQ=^AED (2 góc tương ứng) hay ^BAM=^AEN
Xét \(\Delta\)ABM và \(\Delta\)EAN: ^BAM=^AEN; ^ABM=^EAN (Cùng phụ với ^BAH); AB=AE
=> \(\Delta\)ABM=\(\Delta\)EAN (g.c.g) => AM=EN (2 cạnh tương ứng)
Tương tự ta chứng minh AM=DN => DN=EN => N là trung điểm của DE
\(\Delta\)AEC=\(\Delta\)ABD (c.g.c) => EC=BD
\(\Delta\)EMC=\(\Delta\)SMB (c.g.c) => EC=SB
=> BD=SB => Tam giác DBS cân tại B. Do ^SBF là góc ngoài của \(\Delta\)SDB
=> ^SBF=2. ^BDS .
\(\Delta\)EMC=\(\Delta\)SMB => ^MEC=^MSB => EC//SB hay EF//SB => ^SBF=^EFD (So le trong)
=> ^EFD = 2.^BDS (3)
Dễ thấy Bx và Cy là phân giác 2 góc ngoài của tam giác FBC. Chúng cắt nhau tại I
Nên FI là phân giác của ^CFB hay ^EFD => ^DFI=1/2 ^EFD (4)
Từ (3) và (4) => ^BDS=^DFI => DS//FI (2 góc so le trong)
Mà MN là đường trung bình của tam giác EDS => MN//FI (*)
Xét \(\Delta\)OIF:
K là trung điểm OI, G là trung điểm OF => KG là đường trung bình \(\Delta\)OIF => KG//FI (**)
Xét tứ giác BOCF: M; G lần lượt là trung điểm của 2 đường chéo BC và OF
FB giao CO tại D; FC giao BO tại E; N là trung điểm của DE
Tứ đó ta có: 3 điểm G;M;N cùng nằm trên đường thẳng Gauss của tứ giác BOCF
=> G,M,N thẳng hàng (***)
Từ (*); (**) và (***) => 3 điểm M;N;K thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).
ΔAMC=ΔBMQ (c.g.c) => ^MAC=^MQB
Suy ra AC // BQ (2 góc so le trong bằng nhau) => ^BAC+^ABQ=1800 (1)
Ta có: ^BAC+^EAD= 2.^BAC + ^CAE + ^DAB = (^BAC+^CAE) + (^BAC+^DAB) = ^BAE+^CAD=1800 (2)
Từ (1) và (2) => ^BAC+^ABQ=^BAC+^EAD => ^ABQ=^EAD
=> ΔABQ=ΔEAD (c.g.c) = >^BAQ=^AED (2 góc tương ứng) hay ^BAM=^AEN
Xét ΔABM và ΔEAN: ^BAM=^AEN; ^ABM=^EAN (Cùng phụ với ^BAH); AB=AE
=> ΔABM=ΔEAN (g.c.g) => AM=EN (2 cạnh tương ứng)
Tương tự ta chứng minh AM=DN => DN=EN => N là trung điểm của DE
ΔAEC=ΔABD (c.g.c) => EC=BD
ΔEMC=ΔSMB (c.g.c) => EC=SB
=> BD=SB => Tam giác DBS cân tại B. Do ^SBF là góc ngoài của ΔSDB
=> ^SBF=2. ^BDS .
ΔEMC=ΔSMB => ^MEC=^MSB => EC//SB hay EF//SB => ^SBF=^EFD (So le trong)
=> ^EFD = 2.^BDS (3)
Dễ thấy Bx và Cy là phân giác 2 góc ngoài của tam giác FBC. Chúng cắt nhau tại I
Nên FI là phân giác của ^CFB hay ^EFD => ^DFI=1/2 ^EFD (4)
Từ (3) và (4) => ^BDS=^DFI => DS//FI (2 góc so le trong)
Mà MN là đường trung bình của tam giác EDS => MN//FI (*)
Xét ΔOIF:
K là trung điểm OI, G là trung điểm OF => KG là đường trung bình ΔOIF => KG//FI (**)
Xét tứ giác BOCF: M; G lần lượt là trung điểm của 2 đường chéo BC và OF
FB giao CO tại D; FC giao BO tại E; N là trung điểm của DE
Tứ đó ta có: 3 điểm G;M;N cùng nằm trên đường thẳng Gauss của tứ giác BOCF
=> G,M,N thẳng hàng (***)
Từ (*); (**) và (***) => 3 điểm M;N;K thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).


a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC
a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)
bạn vẽ hình kiểu j thế?????