Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) XétΔABC vg tại A
⇒ BC²=AB²+AC²
⇒ BC=17cm
Xét ΔABH và ΔCBA có:
góc AHB= góc CBA
góc B: chung
⇒ ΔABH ∞ ΔCBA (g.g)
⇒ AB/BC=BH/BA
⇒ BH=AB²/BC
⇒ BH=64/17
Xét ΔABH vg tại H
⇒AB²=BH²+AH²
⇒ AH=120/17
b) xét tg AMHN có: góc AMH= góc ANH= góc MAN=90
⇒ tg AMHN là hcn (dhnb)
⇒ AH=MN (t/c hcn)
⇒ MN=120/17
, Ta thấy tam giác AMH đồng dạng tam giác AHB (g.g) suy ra AM/AH = AH/ AB => AM.AB =AH^2
tam giác ANH đồng dạng tam giác AHC (g.g)
=> AN/AH = AH/AC
=> AN.AC = AH^2
suy ra AM.AB = AN.AC.

a) Xét ΔABC vuông tại A ta có:
\(BC^2\)= \(AB^2+AC^2\)
\(BC^2\) = \(8^2+15^2\)
BC = 17 (cm)
Xét ΔHBA và ΔABC ta có:
\(\widehat{AHB}=\widehat{BAC}\) = \(90^0\)
\(\widehat{ABH}=\widehat{ABC}\) (góc chung)
=> ΔHBA~ΔABC (g-g)
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}=\dfrac{AH}{AC}\) (tsdd)
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
=> \(AB^2=BH.BC\)
=> \(8^2=17.BH\)
=> BH = \(\dfrac{64}{17}\) (cm)
Lại có: \(\dfrac{AB}{BC}=\dfrac{AH}{AC}\) (cmt)
=> \(\dfrac{8}{17}=\dfrac{AH}{15}\)
=> AH = \(\dfrac{120}{17}\) (cm)
b) Xét tg AMNH ta có:
\(\widehat{MAN}=90^0\) (ΔABC vuông tại A)
\(\widehat{AMH}=90^0\) (M là hình chiếu của H lên AB)
\(\widehat{ANH}=90^0\) (N là hình chiếu của H lên AC)
=> Tg AMNH là hcn
Ta có: \(\left\{{}\begin{matrix}AH=\dfrac{120}{17}\\AH=MN\end{matrix}\right.\)
=> MN = \(\dfrac{120}{7}\)
c) Xét ΔAMH và ΔAHB ta có:
\(\widehat{MAH}=\widehat{BAH}\) (góc chung)
\(\widehat{AMH}=\widehat{AHB}\) = \(90^0\)
=> ΔAMH ~ ΔAHB (g-g)
=> \(\dfrac{AM}{AH}=\dfrac{AH}{AB}\) (tsdd)
=> \(AH^2=AM.AB\)
Tương tự như trên xét ΔANH và ΔAHC
=> \(\dfrac{AN}{AH}=\dfrac{AH}{AC}\) (tsdd)
=> \(AH^2=AN.AC\)
=> đpcm (=\(AH^2\))

( Hình ảnh chỉ mang tính chất minh họa )
a) Tính BC và AH :
Tam giác ABC vuông tại A, áp dụng định lý Pytago vào tam giác ABC :
AB2+AC2=BC2
82+152=BC2
⇒BC=17(cm)
Ta có : SABC=12⋅AB⋅AC=12⋅AH⋅BC
⇔AH=AB⋅ACBC=8⋅1517=12017(cm)
b) Có Aˆ=900(giả thiết), Mˆ=900(hình chiếu), Nˆ=900(hình chiếu)
=> Tứ giác AMHN là hình chữ nhật (tứ giác có 3 góc bằng 90 độ).
Vì tứ giác AMHN là hình chữ nhật => Hai đường chéo bằng nhau.
⇒MN=AH=12017(cm)
c) Vì N là hình chiếu của H trên AC ⇒N∈AC
mà MH//AN(hcn) => MH//AC
Theo hệ quả của định lý Ta-let => AMAB=ANAC
Suy ra : AM⋅AC=AN⋅AB(đpcm)

Bài 1:
a: BC=17cm
AH=120/7(cm)
b: Xét tứ giác AMHN có góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
Suy ra: AH=MN=120/7(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nen \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

a, Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow BC^2=64+225=289\Rightarrow BC=17\)cm
Xét tam giác AHC và tam giác BAC ta có :
^AHC = ^BAC = 900
^C _ chung
Vậy tam giác AHC ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{AH}{AB}=\frac{AC}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{8.15}{17}=\frac{120}{17}\)cm
b, Vì MH vuông AB
NA vuông AB
=> MH // NA tương tự ta có : MH // AN
=> tứ giác AMNH là hình bình hành
mà ^HNA = 900 ; ^BAC = 900 ; ^HMA = 900
=> tứ giác AMHN là hình vuông

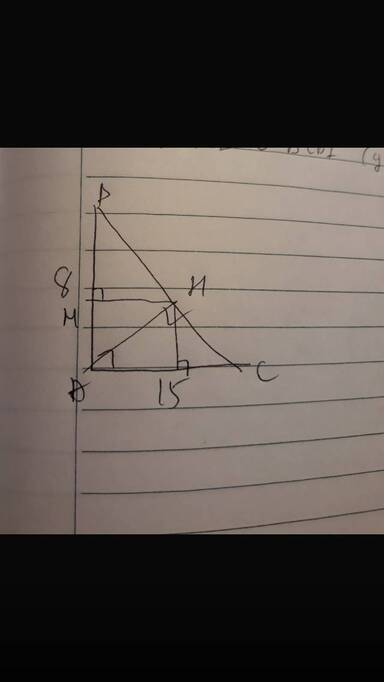


c, Xét tam giác AMH và tam giác AHB có
^A _ chung ; ^AMH = ^AHB = 900
Vậy tam giác AMH ~ tam giác AHB (g.g)
\(\frac{AM}{AH}=\frac{AH}{AB}\Rightarrow AH^2=AM.AB\)
Xét tam giác AHN và tam giác ACH có
^A _ chung ; ^ANH = ^AHC = 900
Vậy tam giác AHN ~ tam giác ACH (g.g)
\(\frac{AH}{AC}=\frac{AN}{AH}\Rightarrow AH^2=AN.AC\)
\(\Rightarrow AM.AB=AN.AC\)