Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)vì tg abc vuông tại a=> AM=\(\dfrac{1}{2}BC\) =BM=MC
xét tg AMF và tg CMF có:
góc F=90 độ
AM=MC
MF:chung
=> tg AMF= tg CMF(ch-cgv)
=>AF=FC=\(\dfrac{1}{2}AC=3\)cm
xét tg BME và tg AME có:
góc E=90 độ
EM: chung
AM=BM
=>tg BME=tg AME(ch-cgv)
=>AE=BE=\(\dfrac{1}{2}AB=2cm\)
diện tích hcn là:
S=AE.AF=2.3=6\(cm^2\)

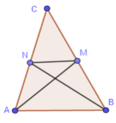
Ta có ABMN là tứ giác có hai đường chéo AM và BN vuông góc
nên có diện tích là: SABMN = 1 2 AB.MN
Hai tam giác AMC và ABC có chung đường cao hạ từ A
nên S A M C S A B C = M C B C = 1 2
=> SAMC = 1 2 SABC (1)
Hai tam giác AMN và AMC có chung đường cao hạ từ M
nên S A M N S A M C = A N A C = 1 2
=> SAMB = 1 2 SABC (2)
Từ (1) và (2) suy ra SAMN = 1 4 SABC
Hai tam giác AMB và ABC có chung đường cao hạ từ A
nên S A M B S A B C = B M B C = 1 2
=> SAMB = 1 2 SABC
Ta có: SABMN = SAMN + SABM
= 1 4 SABC + 1 2 SABC = 3 4 SABC
=> SABC = 4 3 SABMN = 4 3 .AM. 1 2 BN = 2 3 AM.BN
Đáp án cần chọn là: D

a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: \(AE=\dfrac{AB}{2}=\dfrac{4}{2}=2\left(cm\right)\)
AF=AC/2=3cm
Do đó: \(S_{AEMF}=2\cdot3=6\left(cm^2\right)\)
c: Xét ΔCAB có
M là trung điểm của BC
MF//AB
Do đó F là trung điểm của AC
Xét tứ giác AMCK có
F là trung điểm chung của AC và MK
nên AMCK là hình bình hành
mà MA=MC
nên AMCK là hình thoi

a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: \(AE=\dfrac{AB}{2}=\dfrac{4}{2}=2\left(cm\right)\)
AF=AC/2=3cm
Do đó: \(S_{AEMF}=2\cdot3=6\left(cm^2\right)\)
c: Xét ΔCAB có
M là trung điểm của BC
MF//AB
Do đó F là trung điểm của AC
Xét tứ giác AMCK có
F là trung điểm chung của AC và MK
nên AMCK là hình bình hành
mà MA=MC
nên AMCK là hình thoi
\(S=\dfrac{3\cdot4}{2}=6\left(cm^2\right)\)
\(AM=\dfrac{BC}{2}=\dfrac{\sqrt{AB^2+AC^2}}{2}=\dfrac{\sqrt{3^2+4^2}}{2}=2.5\left(cm\right)\)