Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b, Vì K thuộc đường tròn ngoại tiếp tam giác DEF nên tứ giác DKEF nội tiếp
→PKE = PFD (góc ngoài tứ giác)
mà DPF chung
→ΔPKE đồng dạng ΔPFD (góc-góc)
→\(\dfrac{PK}{PE}=\dfrac{PF}{PD}\)
→PK.PD=PF.PE (1)
Vì tứ giác NMFE là tứ giác nội tiếp
→PNE =PFD
mà MPF chung
→ΔPNE đồng dạng ΔPFM (góc-góc)
→\(\dfrac{PN}{PE}=\dfrac{PF}{PM}\) (2 góc tương ứng)
→PN.PM=PE.PF (2)
Từ (1) và (2) suy ra:PN.PM=PK.PD(đpcm)
c) Mình ghi có hơi gọn tí ở một số bước (do đây là những bài toán cơ bản, có thể tự chứng minh được), bạn thông cảm nha!
ENMF nội tiếp và DNHM nội tiếp
\(\Rightarrow PE.PF=PN.PM=PK.PD\) hay \(PN.PM=PK.PD \Rightarrow \) DKNM nội tiếp
\(\Rightarrow\) DKNHM nội tiếp hay DKHM nội tiếp
\(\Rightarrow \widehat{DKH}=180^{\circ}-\widehat{DMH}=180^{\circ}-90^{\circ}=90^{\circ}\) hay \(HK \perp PD\)
Kẻ đường kính DA của đường tròn ngoại tiếp \(\Delta DEF\)
\(\Rightarrow\) EHFA là hình bình hành (bài toán quen thuộc)
Hay H, Q, A thẳng hàng
\(\Delta AKD\) nội tiếp đường tròn đường kính AD nên tam giác này vuông tại K
\(\Rightarrow AK\perp PD\) mà \(HK \perp PD\)
\(\Rightarrow \) A, H, K thẳng hàng mà H, Q, A thẳng hàng
\(\Rightarrow\) Q, H, K thẳng hàng
\(\Rightarrow QK \perp PD\) mà \(DH \perp PQ\)
\(\Rightarrow PH \perp DQ (đpcm)\)

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

d)
Trên BF lấy điểm G sao cho GK //AB
=>KG⊥⊥CE (1) và BGBF=AKAFBGBF=AKAF (2)
theo câu c), DH là phân giác trong ˆKDFKDF^ (3)
=>HKHF=DKDFHKHF=DKDF (4)
có DA⊥⊥DH (5)
từ (3, 5) =>DA là phân giác ngoài ˆKDFKDF^
=>AKAF=DKDFAKAF=DKDF (6)
từ (2, 4, 6) =>BGBF=HKHFBGBF=HKHF (7)
trên tia đối tia BC lấy điểm J sao cho BJ =BG
=>BJBF=BGBFBJBF=BGBF (8)
từ (7, 8) =>BJBF=HKHFBJBF=HKHF
=>JK // BH
=>JK⊥⊥AC (8)
từ (1, 8) =>ˆJKG=ˆACHJKG^=ACH^ (9)
và có JF⊥⊥AH và (1)=>ˆKGJ=ˆCHAKGJ^=CHA^ (10)
từ (9, 10) =>△KGJ∼△CHA△KGJ∼△CHA (g, g)
=>KGCH=GJHA=2.GB2.HI=GBHIKGCH=GJHA=2.GB2.HI=GBHI (11)
từ (10, 11) =>△KGB∼△CHI△KGB∼△CHI (c, g, c)
=>ˆKBF=ˆCIFKBF^=CIF^
=>△FBK∼△FIC△FBK∼△FIC (đpcm)
và ˆICB+ˆFBKICB^+FBK^
=ˆBKF+ˆFBK=90∘=BKF^+FBK^=90∘
=>BK⊥CIBK⊥CI =>K là trực tâm của tam giác IBC (đpcm)
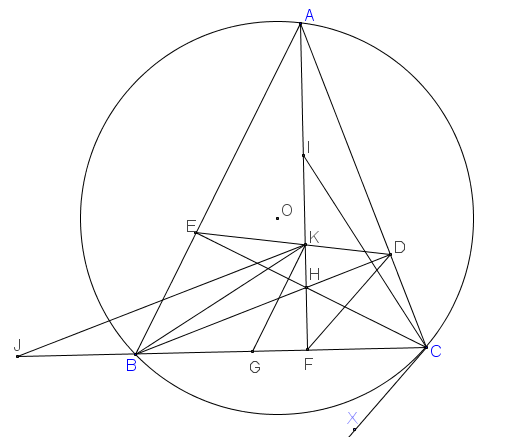
Hình gửi kèm