Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Xét tam giác END và tam giác MND, có
\(\widehat{MND}=\widehat{DNE}=30^o\)(vì ND là tia phân giác)
\(\widehat{M}=\widehat{E}=90^o\)
ND là cạnh chung
\(\Rightarrow\Delta END=\Delta MND\)
\(\RightarrowĐPCM\)

a) Xét ΔMND vuông tại M và ΔHND vuông tại H có
ND chung
\(\widehat{MND}=\widehat{HND}\)(ND là tia phân giác của \(\widehat{MNH}\))
Do đó: ΔMND=ΔHND(cạnh huyền-góc nhọn)

a: Xét ΔMNK và ΔMIK có
MN=MI
góc NMK=góc IMK
MK chung
=>ΔMNK=ΔMIK
=>KN=KI
=>ΔKNI cân tại K
b: ΔMNK=ΔMIK
=>góc MIK=góc MNK=90 độ
b: Xét ΔMEP có
EI,PN là đường cao
EI cắt PN tại K
=>K là trực tâm
=>MK vuông góc EP

a: NP^2=MN^2+MP^2
=>ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>DM=DE

a) Xét \(\Delta MNK\left(\widehat{M}=90^o\right)\) và \(\Delta QNK\left(\widehat{Q}=90^o\right)\) có:
\(\widehat{MNK}=\widehat{QNK}\) (giả thiết)
\(NK\) là cạnh chung
\(\Rightarrow\Delta MNK=\Delta QNK\left(ch.gn\right)\)
b) Vì \(\Delta MNK=\Delta QNK\left(cmt\right)\)
\(\Rightarrow MN=QN\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta MNQ\) cân tại \(N\)
Mà \(\widehat{MNQ}=60^o\)
\(\Rightarrow\Delta MNQ\) đều
Vì \(NK\) là tia phân giác \(\widehat{MNP}\) (giả thiết)
\(\Rightarrow\widehat{MNK}=\widehat{QNK}=\dfrac{\widehat{MNP}}{2}=\dfrac{60^o}{2}=30^o=\widehat{NPK}\)
\(\Rightarrow\Delta NKP\) cân tại \(K\)
c) Vì \(\Delta NMQ\) đều (chứng minh trên)
\(\Rightarrow NM=MQ=NQ=8cm\)
Xét \(\Delta NMP\left(\widehat{M}=90^o\right)\) có:
\(PN=2MN=2.8=16cm\)
\(\Rightarrow PQ=16-8=8cm\)
a: Xét ΔMNK vuông tại M và ΔQNK vuông tại Q có
NK chung
\(\widehat{MNK}=\widehat{QNK}\)
Do đó: ΔMNK=ΔQNK
b: Ta có: ΔMNK=ΔQNK
nên NM=NQ
=>ΔNMQ cân tại N
mà \(\widehat{MNQ}=60^0\)
nên ΔMNQ đều
Xét ΔNKQ có
\(\widehat{KPN}=\widehat{KNP}\)
nên ΔNKQ cân tại K
c: Xét ΔMNP vuông tại M có
\(\cos N=\dfrac{MN}{NP}\)
=>NP=16(cm)
=>\(MP=8\sqrt{3}\left(cm\right)\)

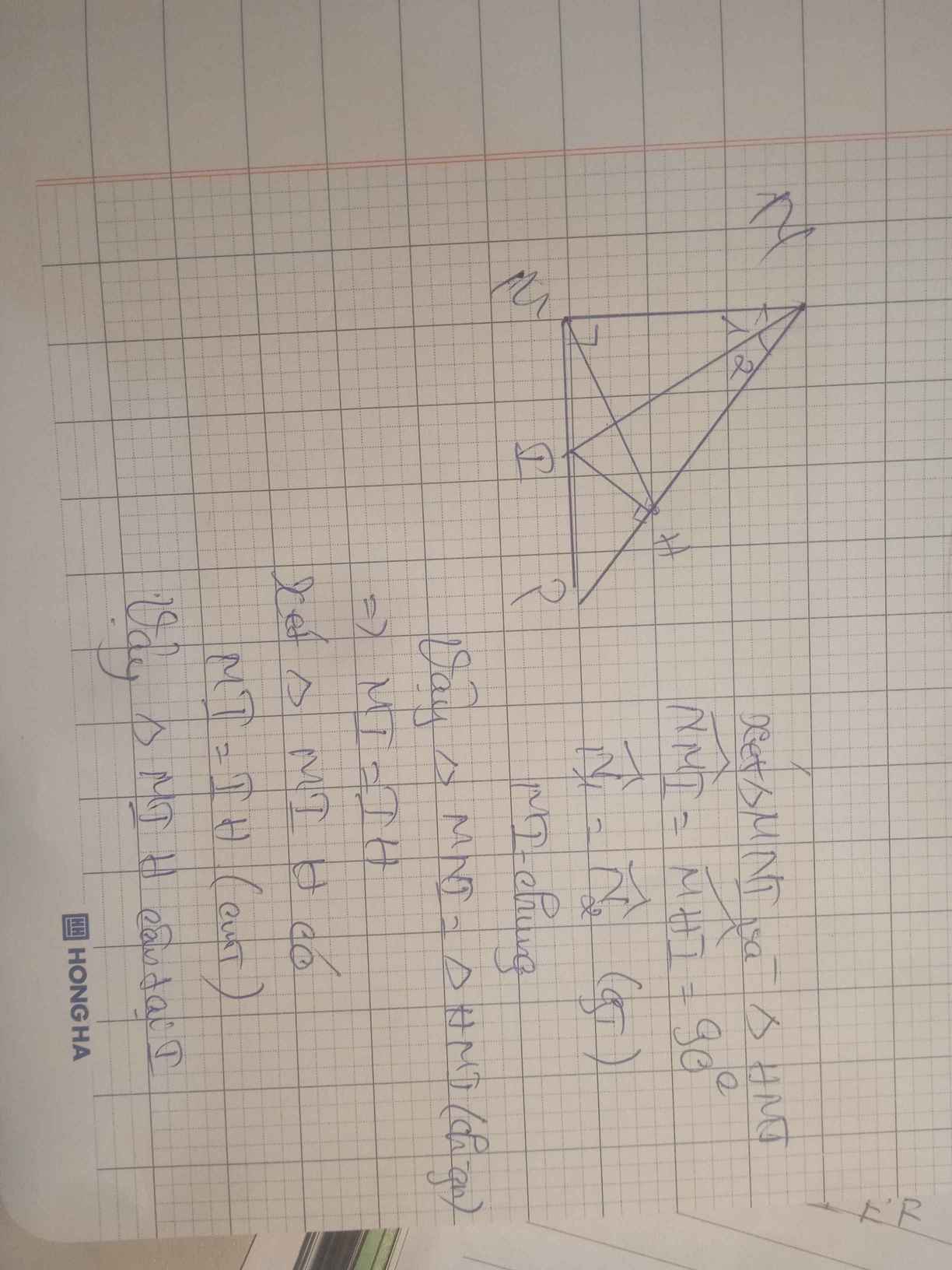
a: Xét ΔMNQ vuông tại M và ΔHNQ vuông tại H có
NQ chung
\(\widehat{MNQ}=\widehat{HNQ}\)
Do đó: ΔMNQ=ΔHNQ
b: ta có: ΔMNQ=ΔHNQ
nên NM=NH
hay ΔNHM cân tại N
mà \(\widehat{MNH}=60^0\)
nên ΔNHM đều