Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn chỉ cần chứng minh AEDM là HCN ;O là trung điểm của DE =>O cũng là trung điểm của AM =>O,M,A thẳng hàng
b,
Gọi P ,Q lần lượt là trung điểm của AB,AC
=> giới hạn :
*Khi M trùng với B=> O trùng với P
*Khi M trùng với C=> O trùng với Q
=> I thuộc PQ
c,
Kẻ đường cao AH
Khi M trùng với H thì AM ngắn nhất (quan hệ đường vuông góc và đường xiên)

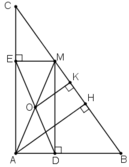
a) Tứ giác ADME có: 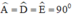
⇒ ADME là hình chữ nhật
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC.
Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH
⇒ OK là đường trung bình của ΔMAH
⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.

Bài giải:
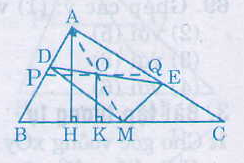
a) Tứ giác ADME có ˆA=ˆD=ˆE=900A^=D^=E^=900
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
b)Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Cách 1:
Kẻ OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC).
Suy ra OK=12AHOK=12AH
Điểm O cách đoạn BC cố định một khoảng không đổi bằng 12AH12AH. Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB. Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
Cách 2: Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.

a) Tứ giác ADME có ˆA=ˆD=ˆE=900A^=D^=E^=900
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
b)Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Cách 1:
Kẻ OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC).
Suy ra OK=12AHOK=12AH
Điểm O cách đoạn BC cố định một khoảng không đổi bằng 12AH12AH. Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB. Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
Cách 2: Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.
=

bạn nên viết kí hiệu đối với từ vuông góc, góc, độ, tam giác
a)có MD vuông góc với AB(gt)=>góc ADM=90 độ
ME vuông góc với DM(gt)=>góc MDE=90 độ
có góc ADM=góc DME=góc A=90 độ
=>ADME là hình chữ nhật
mà DE là đường chéo(do AM cắt DE tại O)
=>O là trug điểm
=>A,O,M thag hag
b. vẽ AH và OK vuông góc và đặt AH=a(ko đổi)
trong tam giác AHM có OK là dduong trug binh
=>OK=AH/2=a/2(ko đổi)
Vậy M di chuyen tren BC thi diem O di chuyen tren doan thag d nam trog tam giác ABC và cách cạch chuyền BC 1 khoag =a/2
c.Khi điểm M trung với điểm H, nghĩa là AM=AH thì khi do AM có do dai nho nhatvi duog cao bao gio cung ngan hon cac duog xiên cung xuat phat tu 1 diem den duong thang)
Xét \(\Delta MBD\)cân tại M có :
\(\widehat{BDM}=60^0\)
\(\Rightarrow\Delta MBD\)là tam giác đều
\(\Rightarrow\widehat{BDM}=60^0\)
\(\Rightarrow\widehat{BDA}=120^0\)
\(\Rightarrow\)Khi M di chuyển trên cung nhỏ BC thì M di chuyển trên cung tròn ( nằm trên nửa mặt phẳng bờ AB chưa điểm M ) nhìn AB một góc bằng \(120^0\)
Xét \(\Delta DBA\)và \(\Delta MBC\)có :
\(BA=BC\)( vì tam giác ABC đều )
\(\widehat{BAD}=\widehat{BCM}\)( cùng chắn cung BM )
\(\widehat{ABD}=\widehat{CBM}\left(=60^0-\widehat{DBC}\right)\)
Suy ra \(\Delta DBA=\Delta MBC\)
\(\Rightarrow MC=DA\)
\(\Rightarrow MA+MB+MC=MA+MD+DA=2MA\)
\(MA+MB+MC\)lớn nhất khi MA lớn nhất
\(\Rightarrow AM\)là đường kính của \(\left(O\right)\)
\(\Rightarrow M\)là điểm chính giữa của cung BC
Chúc bạn học tốt !!!