Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|\overrightarrow{AM}\right|=AM=\dfrac{a\sqrt{3}}{2}\)

Lời giải:
\(\overrightarrow{AC}.\overrightarrow{BI}=(\overrightarrow{AM}+\overrightarrow{MC})(\overrightarrow{BM}+\overrightarrow{MI})\)
\(=\overrightarrow{AM}.\overrightarrow{BM}+\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}+\overrightarrow{MC}.\overrightarrow{MI}\)
\(=\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}\)
\(=\overrightarrow{AM}.\frac{-\overrightarrow{AM}}{2}+\frac{\overrightarrow{BC}}{2}.\overrightarrow{BC}=\frac{BC^2-AM^2}{2}\)
\(=\frac{BC^2-(\frac{\sqrt{3}}{2}BC)^2}{2}=\frac{BC^2}{8}=\frac{9a^2}{8}\)

1.
Gọi M là trung điểm BC thì theo tính chất trọng tâm: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\Rightarrow x+y=\dfrac{2}{3}\)
2.
\(CH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(T=\left|\text{ }\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(\Rightarrow T^2=CA^2+CH^2+2\overrightarrow{CA}.\overrightarrow{CH}=a^2+\left(\dfrac{a}{2}\right)^2+2.a.\dfrac{a}{2}.cos60^0=\dfrac{7a^2}{4}\)
\(\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(10< x< 100\Rightarrow10< 3k< 100\)
\(\Rightarrow\dfrac{10}{3}< k< \dfrac{100}{3}\Rightarrow4\le k\le33\)
\(\Rightarrow\sum x=3\left(4+5+...+33\right)=1665\)

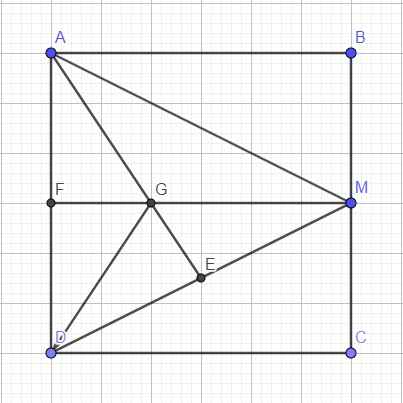
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??
\(\left|\overrightarrow{CH}+\overrightarrow{CH}\right|=a\)