Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

...............................................................................
..........................................................................................
...........................................................................tgbvn JGKGITJNNFJFJNFJBFÒNBFOHRJ;FFJh' IIIor ỉie

Xét \(\left(\dfrac{EK}{2}\right)\) có
ΔKME nội tiếp đường tròn
KE là đường kính
Do đó: ΔKME vuông tại M
Xét \(\left(\dfrac{FK}{2}\right)\) có
ΔFNK nội tiếp đường tròn
FK là đường kính
Do đó: ΔFNK vuông tại N
Xét tứ giác DMKN có \(\widehat{DMK}=\widehat{DNK}=\widehat{MDN}=90^0\)
nên DMKN là hình chữ nhật
hay D,M,K,N cùng thuộc 1 đường tròn

b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

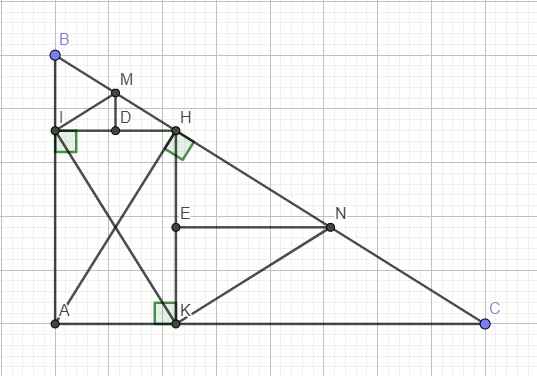
a. Ta có tứ giác AIHK là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow\widehat{IKH}=\widehat{IAH}\)
Mà \(\widehat{IAH}=\widehat{KCH}\) (cùng phụ \(\widehat{ABC}\))
\(\Rightarrow\widehat{IKH}=\widehat{KCH}\)
b.
Gọi D và E lần lượt là trung điểm IH và HK
\(\Rightarrow\) MD và NE lần lượt là đường trung bình các tam giác BIH và HKC
\(\Rightarrow\left\{{}\begin{matrix}MD\perp HI\\MD=\dfrac{1}{2}BI\end{matrix}\right.\) và \(\left\{{}\begin{matrix}NE\perp HK\\NE=\dfrac{1}{2}CK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}S_{MIH}=\dfrac{1}{2}MD.IH=\dfrac{1}{2}.\dfrac{1}{2}BI.IH=\dfrac{1}{2}S_{BIH}\\S_{NHK}=\dfrac{1}{2}NE.HK=\dfrac{1}{2}.\dfrac{1}{2}CK.HK=\dfrac{1}{2}S_{HCK}\end{matrix}\right.\)
Đồng thời AIHK là hình chữ nhật \(\Rightarrow S_{IHK}=\dfrac{1}{2}S_{AIHK}\)
Do đó:
\(S_{MNKI}=S_{MIH}+S_{NHK}+S_{IHK}=\dfrac{1}{2}\left(S_{BIH}+S_{AIHK}+S_{HCK}\right)=\dfrac{1}{2}S_{ABC}\) (đpcm)