Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)`
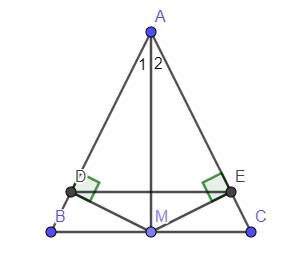
Xét `Delta ABM` và `Delta ACM` có :
`{:(AB=AC(GT)),(AM-chung),(BM=CM(M là tđ BC)):}}`
`=>Delta ABM=Delta ACM(c.c.c)(đpcm)`
`b)`
`Delta ABM=Delta ACM(cmt)=>hat(A_1)=hat(A_2)`
mà `AM` nằm giữa `AB` và `AC`
nên `AM` là p/g của `hat(BAC)(đpcm)`
`c)`
Xét `Delta ADM` và `Delta AEM` có :
`{:(hat(ADM)=hat(AEM)(=90^)),(AM-chung),(hat(A_1)=hat(A_2)(cmt)):}}`
`=>Delta ADM=Delta AEM(ch-gn)`
`=>AD=AE` ( 2 cạnh t/ứng )
`=>Delta ADE` cân tại `A(đpcm)`

a) xét ΔABM và ΔACM có
góc B = góc C
AB = AC ( ΔABC cân tại A )
BM=CM ( tính chất các đường của Δ cân từ đỉnh )
=> ΔABM = ΔACM
b) xét ΔBME và ΔCMF có
góc B bằng góc C
BM=CM
=> ΔBME=ΔCMF ( cạnh huyền góc nhọn )
=> FM = EM
=> ΔEMF cân tại M
c) gọi giao của EF và AM là O
ta có BE = CF => AE=AF
=> ΔAEF cân tại A
ta có AM là tia phân giác của góc A
mà O nằm trên AM suy ra AO cũng là tia phân giác của góc A
ta lại có ΔAEF cân tại A
suy ra AO vuông góc với EF
suy ra AM vuông góc với EF
xét ΔAEF và ΔABC có
EF và BC đều cùng vuông góc với AM => EF // BC