Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cau b)
ta có tgiac abc vuông tại a(gthiet)
theo định lí pi ta go ta có:
BC^2=AC^2+AB^2=81+144=225
suy ra BC=15
*BD=?
ta có AD la p/giac (giả thiết)
suy ra BD/DC=AB/AC (tính chất đương phân giác)
suy ra BD/BD+DC=9/9+12=3/7
suy ra BD/BC=3/7
suy ra BD=15.3/7=45/7
DC=BC-BD=15-45/7=60/7
*Câu c)............

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Vậy: AC=4cm
b) Xét ΔABD vuông tại A và ΔEBC vuông tại E có
\(\widehat{ABD}=\widehat{EBC}\)(BE là tia phân giác của \(\widehat{ABC}\))
Do đó: ΔABD\(\sim\)ΔEBC(g-g)

a: \(BC=\sqrt{4.2^2+5.6^2}=7\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot4.2\cdot5.6=11.76\left(cm^2\right)\)
b: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=7/7=1
=>DB=3cm; DC=4cm
c: Xét ΔCAB có ED//AB
nên ED/AB=CD/CB
=>ED/4,2=4/7
=>ED=2,4cm

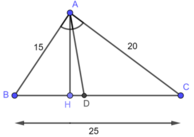
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)