Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý phân giác:
BDCD=ABAC=23⇒3BD=2CD=2(BC−BD)BDCD=ABAC=23⇒3BD=2CD=2(BC−BD)
⇔5BD=2BC⇒BD=25BC⇒BDBC=25⇔5BD=2BC⇒BD=25BC⇒BDBC=25
AE=35AD=35(AE+DE)⇒2AE=3DE⇒DEAE=23AE=35AD=35(AE+DE)⇒2AE=3DE⇒DEAE=23
Qua D kẻ đường thẳng song song AC cắt AE tại F
Áp dụng định lý Talet:
FDAK=FEKE=DEAE=23FDAK=FEKE=DEAE=23
Talet cho tam giác BCK: FDCK=BDBC=25FDCK=BDBC=25
⇒(FDAK):(FDCK)=(23):(25)⇔CKAK=53⇒(FDAK):(FDCK)=(23):(25)⇔CKAK=53
⇒CKAC−CK=53⇒3CK=5(24−CK)⇒CK=15⇒CKAC−CK=53⇒3CK=5(24−CK)⇒CK=15
AK=AC−CK=9

Áp dụng định lý phân giác:
\(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{2}{3}\Rightarrow3BD=2CD=2\left(BC-BD\right)\)
\(\Leftrightarrow5BD=2BC\Rightarrow BD=\dfrac{2}{5}BC\Rightarrow\dfrac{BD}{BC}=\dfrac{2}{5}\)
\(AE=\dfrac{3}{5}AD=\dfrac{3}{5}\left(AE+DE\right)\Rightarrow2AE=3DE\Rightarrow\dfrac{DE}{AE}=\dfrac{2}{3}\)
Qua D kẻ đường thẳng song song AC cắt AE tại F
Áp dụng định lý Talet:
\(\dfrac{FD}{AK}=\dfrac{FE}{KE}=\dfrac{DE}{AE}=\dfrac{2}{3}\)
Talet cho tam giác BCK: \(\dfrac{FD}{CK}=\dfrac{BD}{BC}=\dfrac{2}{5}\)
\(\Rightarrow\left(\dfrac{FD}{AK}\right):\left(\dfrac{FD}{CK}\right)=\left(\dfrac{2}{3}\right):\left(\dfrac{2}{5}\right)\Leftrightarrow\dfrac{CK}{AK}=\dfrac{5}{3}\)
\(\Rightarrow\dfrac{CK}{AC-CK}=\dfrac{5}{3}\Rightarrow3CK=5\left(24-CK\right)\Rightarrow CK=15\)
\(AK=AC-CK=9\)

Theo tính chất phân giác: \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{BD}{BD+CD}=\dfrac{AB}{AB+AC}=\dfrac{16}{16+24}=\dfrac{2}{5}\Rightarrow\dfrac{BD}{BC}=\dfrac{2}{5}\)
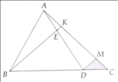
Kẻ DM//BK với \(M\in AC\)
Trong tam giác ADM, áp dụng talet: \(\dfrac{AK}{KM}=\dfrac{AE}{ED}=\dfrac{3}{2}\)
Trong tam giác CBK, áp dụng talet: \(\dfrac{KM}{KC}=\dfrac{BD}{BC}=\dfrac{2}{5}\)
\(\Rightarrow\dfrac{AK}{KM}.\dfrac{KM}{KC}=\dfrac{3}{2}.\dfrac{2}{5}=\dfrac{3}{5}\Rightarrow\dfrac{AK}{KC}=\dfrac{3}{5}\Rightarrow AK=\dfrac{3}{5}KC\)
Mà \(AK+KC=AC=24\Rightarrow\dfrac{3}{5}KC+KC=24\)
\(\Rightarrow\dfrac{8}{5}KC=24\Rightarrow KC=15\)
\(\Rightarrow AK=\dfrac{3}{5}KC=9\)