Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
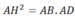



Lời giải:
Bạn tự vẽ hình giùm mình nhé.
a) Xét tam giác $BAC$ và $BHA$ có:
\(\left\{\begin{matrix} \widehat{BAC}=\widehat{BHA}=90^0\\ \text{chung góc B}\end{matrix}\right.\Rightarrow \triangle BAC\sim \triangle BHA(g.g)\)
b)
Xét tam giác $BAC$ và $AHC$ có:
\(\left\{\begin{matrix} \widehat{BAC}=\widehat{AHC}=90^0\\ \text{chung góc C}\end{matrix}\right.\Rightarrow \triangle BAC\sim \triangle AHC(g.g)\)
\(\Rightarrow \frac{BC}{AC}=\frac{AC}{HC}\Rightarrow AC^2=BC.HC\)
c)
Xét tam giác $HEA$ và $BHA$ có:
\(\left\{\begin{matrix} \widehat{HEA}=\widehat{BHA}=90^0\\ \widehat{EHA}=\widehat{HBA}(=90^0-\widehat{BHE})\end{matrix}\right.\)
\(\Rightarrow \triangle HEA\sim \triangle BHA(g.g)\)
\(\Rightarrow \frac{HA}{EA}=\frac{BA}{HA}\Rightarrow HA^2=AE.AB(1)\)
Hoàn toàn TT ta có: \(\triangle HFA\sim \triangle CHA\Rightarrow \frac{HA}{FA}=\frac{CA}{HA}\)
\(\Rightarrow HA^2=AF.AC(2)\)
Từ \((1)(2)\Rightarrow AF.AC=AE.AB\Rightarrow \frac{AE}{AF}=\frac{AC}{AB}\)
Tam giác $AFE$ và $ABC$ có:
\(\left\{\begin{matrix} \frac{AE}{AF}=\frac{AC}{AB}\\ \text{chung góc A}\end{matrix}\right.\Rightarrow \triangle AFE\sim \triangle ABC(c.g.c)\)
d)
Có: \(\widehat{MEB}=\widehat{AEF}=\widehat{ACB}\) (do \(\triangle AFE\sim \triangle ABC\) )
Xét tam giác $MEB$ và $MCF$ có:
\(\left\{\begin{matrix} \text{chung góc M}\\ \widehat{MEB}=\widehat{MCF}\end{matrix}\right.\Rightarrow \triangle MEB\sim \triangle MCF(g.g)\)
\(\Rightarrow \frac{ME}{MB}=\frac{MC}{MF}\Rightarrow ME.MF=MB.MC\)

a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat{HAB}=\widehat{BAC}=90^0\)
\(\widehat{B}:chung\)
do đó \(\Delta HBA\sim\Delta ABC\left(g-g\right)\)
b) Xét \(\text{ΔHBAvàΔHAC}\) có:
\(\widehat{BHA}=\widehat{CHA}=90^o\)
\(\widehat{ABH}=\widehat{HAC}\) ( do cùng phụ với \(\widehat{BAH}\))
Do đó: \(\Delta HBA\sim\Delta HAC\left(g-g\right)\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB\cdot HC\)
c) Xét tứ giác ADHE có:
\(\widehat{A}=\widehat{D}=\widehat{E}=90^o\)
Do đó ADHE là hình chữ nhật
Gọi O là giao điểm 2 đường chéo hình chữ nhật(AH và DE)
\(\Rightarrow OD=OA\)(tính chất HCN)
\(\Rightarrow\Delta ODA\) cân tại O
\(\Rightarrow\widehat{ODA}=\widehat{OAD}\)
Xét \(\Delta ADE\) và \(\Delta HAB\) có:
\(\widehat{BHA}=\widehat{DAE}=90^o\\ \widehat{ODA}=\widehat{OAD}\left(cmt\right)\\ \Rightarrow\Delta ADE\sim\Delta HAB\)
Mà \(\Delta HBA\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\) (tính chất bắc cầu)
