Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a
Do \(MN//BC\) nên theo định lý Thales ta có:\(\frac{AN}{NC}=\frac{AM}{MB}=\frac{MN}{BC}\)
\(\Rightarrow\frac{8}{NC}=\frac{3}{2}\Rightarrow NC=\frac{16}{3}\)
Áp dụng định Pythagoras ta có:\(AM^2+AN^2=MN^2\Rightarrow MN=\sqrt{AM^2+AN^2}=10\)
Mà \(\frac{AM}{MB}=\frac{MN}{BC}\Rightarrow\frac{3}{2}=\frac{10}{BC}\Rightarrow BC=\frac{20}{3}\)
b
Hạ \(NH\perp BC;MG\perp BC\)
Áp dụng định lý Pythagoras vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2=\sqrt{BC^2-AC^2}\Rightarrow AB=\sqrt{10-\left(\frac{16}{3}\right)^2-8^2}=\frac{2\sqrt{17}}{3}\)
Bạn áp dụng định lý Ta Lét ( do ND//AB ) rồi tính được ND
Diện tích tam giác vuông NCD sẽ tính bằng \(\frac{NC\cdot ND}{2}\) ( do đã biết được ND và NC )
Lại có \(S_{NCD}=\frac{NH\cdot CD}{2}\) rồi tính được NH.
Do NH=MG nên tính được diện tích hình bình hành BMND.Hướng là thế đấy,bạn làm tiếp nha,mik nhác quá:(

a) Xét ΔABC có
MN//BC(gt)
Do đó: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)(Định lí Ta lét)
Suy ra: \(\dfrac{6}{4}=\dfrac{8}{NC}\)
hay \(NC=\dfrac{16}{3}cm\)
Ta có: AM+MB=AB(M nằm giữa A và B)
nên AB=6+4=10(cm)
Ta có: AN+NC=AC(N nằm giữa A và C)
nên \(AC=8+\dfrac{16}{3}=\dfrac{40}{3}cm\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{40}{3}\right)^2=\dfrac{2500}{9}\)
hay \(BC=\dfrac{50}{3}cm\)
Xét ΔABC có
MN//BC(gt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{\dfrac{50}{3}}=\dfrac{6}{10}\)
\(\Leftrightarrow MN=\dfrac{6\cdot\dfrac{50}{3}}{10}=\dfrac{100}{10}=10cm\)
Vậy: MN=10cm; \(NC=\dfrac{16}{3}cm\); \(BC=\dfrac{50}{3}cm\)

:V chụp xong không gửi được cái phần kia nên mình chép ra vậy hình bạn tự vẽ nhé v
a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Xét tam giác ABC có MN//BC (gt)
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{3}{4}=\frac{AN}{8}=\frac{MN}{10}\)
\(\Rightarrow\hept{\begin{cases}AN=6\left(cm\right)\\MN=7,5\left(cm\right)\end{cases}}\)
b)Vì MI//AC (gt)
\(\Rightarrow MI//AK\left(K\in AB\right)\)
Vì IK//AB(gt)
\(\Rightarrow IK//AM\left(M\in AB\right)\)
Ta có: \(\hept{\begin{cases}MI//AK\left(cmt\right)\\IK//AM\left(cmt\right)\end{cases}\Rightarrow MI=AK}\)( tc cặp đoạn chắn)
Ta có: AM+MB=AB
\(\Rightarrow MB=1,5\left(cm\right)\)
Xét tam giác ABC có MI//AB(gt)

Cho biểu thức B=\(\frac{2x+1}{x^2-1}\); A= \(\frac{3x+1}{x^2-1}\)--\(\frac{x}{x-1}\)+\(\frac{x-1}{x+1}\) (x khác +,- 1; x khác \(\frac{-1}{2}\))
a) Tính giá trị của B biết x=-2
b) Rút gọn A
c) Cho P=A:B Tìm x biết P=3
Cho biểu thức A=\(\left(\frac{2x-3}{x^2-9}-\frac{2}{x+3}\right):\frac{x}{x+3}\)(x khác +,- 3)
a) Rút gọn A
b) TÍnh giá trị của A khi x=\(-\frac{1}{2}\)
c) Tìm các giá trị nguyên của x để A nhận giá trị nguyên

M nằm giữa A và B nên: AB = AM + MB = 10cm
Theo định lí Ta let ta có:
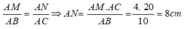
Chọn đáp án A

a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: MN//BC
=>AM/AB=MN/BC
=>MN/7,5=2/3
=>MN=5cm
BM=AB-AM=2cm
Xét ΔABC có MN//BC
nên AM/MB=AN/NC
=>3/NC=2
hay NC=1,5(cm)
=>CA=4,5(cm)
\(BC=\sqrt{6^2+4.5^2}=7.5\left(cm\right)\)