Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Tự vẽ hình
a) Xét tam giác MAB và MDC có :
MA=MD(GT)
BM=CM(GT)
\(\widehat{BMA}=\widehat{DMC}\left(đđ\right)\)
=> Tam giác MAB=MDC ( c.g.c )
b) Mình nghĩ đề bài sửa thành CM AB//CD thì có vẻ đúng hơn
Có : Tam giác MAB=MDC (cmt)
=> \(\widehat{BAD}=\widehat{ADC}\)
Mà 2 góc này ở vị trí so le trong
=> AB//CD
- Xét tam giác ABD và CDA có :
AD-cạnh chung
\(\widehat{ADC}=\widehat{DAB}\left(tgMAB=MDC\right)\)
AB=BC(tgMAB=MDC)
=> 2 tam giác này bằng nhau
c) Vâng, như đề bài thì chúng ta đã có tam giác ABC vuông tại A nên khỏi cần chứng minh đâu :)
#Hoctot

#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = ME (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB = CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{BHA}=\widehat{BHD}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`=> AB = BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD = CE`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`HA = HD (g``t)`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HM` chung
`=>` Tam giác `AMH =` Tam giác `DMH (c-g-c)`
`=> AM = DM (2` cạnh tương ứng `)`
Xét Tam giác `AMD` có: `AM = DM`
`->` Tam giác `AMD` là tam giác cân.

a) Vì M là trung điểm BC suy ra BM =CM(1)
Xét tam giác BMN và tam giác CMA có :
BM=CM(1)
Góc BMN = Góc CMA(gt)
MA=MN(gt)
Suy ra tam giác BMN = tam giác CMA (đfcm)
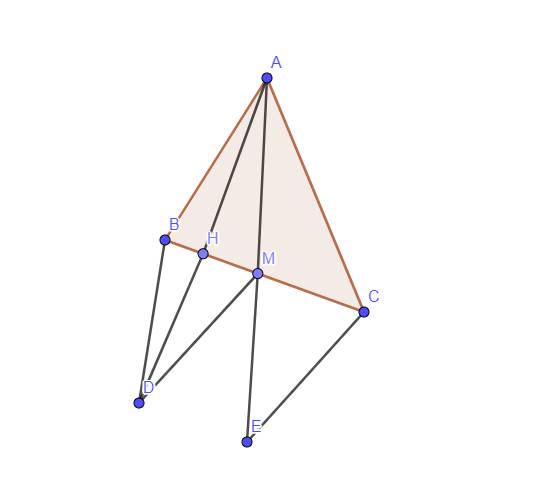
a, xét tam giác AMB và tam giác DMC có : MA = MD (gt)
MC = MB do M là trung điểm của BC (gt)
góc DMC = góc BMA (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
b, tam giác AMB = tam giác DMC (câu a)
=> góc DCM = góc MAB (đn) mà 2 góc này so le trong
=> DC // AB (đl)
c,
https://olm.vn/thanhvien/cuongktl
SÉT \(\Delta AMC\)VÀ\(\Delta DMB\)CÓ
\(AM=DM\left(gt\right)\)
\(\widehat{AMC}=\widehat{DMB}\left(đđ\right)\)
\(MC=MB\left(gt\right)\)
\(\Rightarrow\Delta AMC=\Delta DMB\left(C-G-C\right)\)
TA CÓ\(\Delta MAB+\Delta AMC=\Delta ABC\)
\(\Delta DMB+\Delta MDC=\Delta DCB\)
MÀ \(\Delta AMC=\Delta DMB\left(cmt\right)\)
\(\Delta MAB=\Delta MDC\left(cmt\right)\)
\(\Rightarrow\Delta ABC=\Delta DCB\)
\(\Rightarrow\widehat{A}=\widehat{D}=90^o\)(HAI GÓC TƯƠNG ỨNG)
VẬY \(\Delta BDC\)TAM GIÁC VUÔNG TẠI D