Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tg vuông BAC và tg vuông BHA có
\(\widehat{ACB}=\widehat{BAH}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg BAC đồng dạng với tg BHA (g.g.g)
b/ Xét tg vuông BAC có
\(BC=\sqrt{AB^2+AC^2}\) (Pitago) \(\Rightarrow BC=\sqrt{6^2+8^2}=10cm\)
\(AB^2=HB.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\Rightarrow HC=BC-HB=10-3,6=6,4cm\)
\(AH^2=HB.HC\) (Trong tg vuông bình phương đường cạo hạ từ đỉnh góc vuông bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH^2=3,6.6,4=23,04\Rightarrow AH=4,8cm\)
c/
Xét tg vuông HBM và tg vuông ABD có
\(\widehat{HBM}=\widehat{ABD}\left(gt\right)\) => tg HBM đồng dạng với tg ABD (g.g.g)
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{HM}{AD}\Rightarrow\dfrac{AD}{AB}=\dfrac{HM}{HB}\) (1)
Xét tg vuông ABC có BD là phân giác \(\widehat{B}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}\) (T/c đường phân giác: Trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đợn thẳng tỷ lệ với hai cạnh kề hai đoạn thẳng đó) (2)
Xét tg ABH có BM là phân giác \(\widehat{B}\)
\(\Rightarrow\dfrac{HM}{HB}=\dfrac{AM}{AB}\) (T/c đường phân giác: Trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đợn thẳng tỷ lệ với hai cạnh kề hai đoạn thẳng đó) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{HM}{HB}=\dfrac{AM}{AB}\)
\(\Rightarrow\dfrac{AD}{AB}.\dfrac{AM}{AB}=\dfrac{CD}{BC}.\dfrac{HM}{HB}\)
Mà \(HB.BC=AB^2\) (cmt)
\(\Rightarrow\dfrac{AD.AM}{AB^2}=\dfrac{HM.CD}{AB^2}\Rightarrow AM.AD=HM.CD\)
\(\Rightarrow AM.AD-HM.CD=0\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{DA}{6}=\dfrac{DC}{10}\)
mà DA+DC=AC(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DA}{6}=\dfrac{DC}{10}=\dfrac{DA+DC}{6+10}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{DA}{6}=\dfrac{1}{2}\\\dfrac{DC}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DA=3\left(cm\right)\\DC=5\left(cm\right)\end{matrix}\right.\)
Vậy: DA=3cm; DC=5cm

3:
a: AE/AD=9/6=3/2
AD/AC=6/12=1/2
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng vơi ΔABC
c: IB/IC=AB/AC=AD/AE
=>IB*AE=IC*AD

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AD/DC=BA/BC=6/10=3/5
b: Xét ΔHBA vuông tạiH và ΔABC vuôg tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
màgóc DBC=góc ABD
nên góc AID=góc ADI
=>ΔAID cân tại A

a.
Xét hai tam giác BAC và BHA có:
\(\left\{{}\begin{matrix}\widehat{ABH}\text{ chung}\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BAC\sim\Delta BHA\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\)
Do \(\Delta BAC\sim\Delta BHA\Rightarrow\dfrac{BC}{AB}=\dfrac{AC}{AH}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(BH=\sqrt{AB^2-AH^2}=\dfrac{9}{5}\)
\(CH=BC-BH=\dfrac{16}{5}\)
c.
Do BD là phân giác góc B, áp dụng định lý phân giác cho tam giác ABC:
\(\dfrac{DC}{AD}=\dfrac{BC}{AB}\) (1)
Áp dụng định lý phân giác cho tam giác ABH:
\(\dfrac{AM}{HM}=\dfrac{AB}{BH}\) (2)
Lại có \(\Delta BAC\sim\Delta BHA\Rightarrow\dfrac{BC}{AB}=\dfrac{AB}{BH}\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{DC}{AD}=\dfrac{AM}{HM}\Rightarrow AM.AD=HM.CD\)

a: BC=25cm
Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{20}{8}=2.5\)
Do đó: AD=7,5cm; CD=12,5(cm)
b: \(AH=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(HB=\dfrac{15^2}{25}=9\left(cm\right)\)
d: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
mà góc ABD=góc DBC
nên góc ADI=góc AID
hay ΔAID cân tại A

b) Xét ΔABH có BI là đường phân giác ứng với cạnh AH(Gt)
nên \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\)(Tính chất đường phân giác của tam giác)(1)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{DC}=\dfrac{BA}{BC}\)(Tính chất đường phân giác của tam giác)(2)
Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH∼ΔCBA(g-g)
Suy ra: \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)(đpcm)
Dành cho anh em nào cần phần C nha
Xét ∆HIB và ∆AID có:
Góc IHB= góc IAD
Góc I( đối đỉnh)
Suy ra ∆HIB đồng dạng vs ∆ AID
Suy ra góc HBI = ADI
Mà tâm giác BIH vuông tại H nên Góc HBI = BIH
Mà hai góc I đối đỉnh nên góc HBI = AID
Mà góc HBI = ADI
Nên góc ADI = góc AID
Suy ra tâm giác AID cân (đpcm) (hơi dài nhỉ nhưng có cách ngắn nhưng nó sẽ không chi tiết mong ae thông cảm )
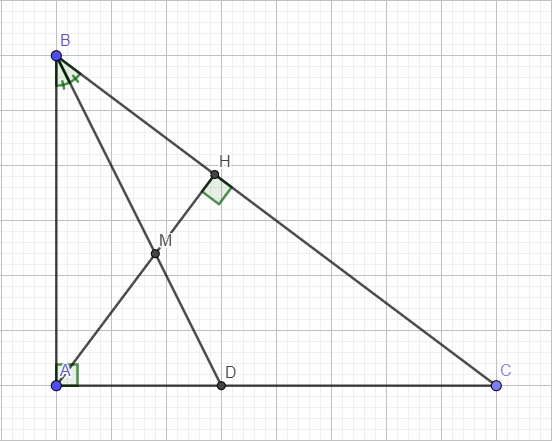
a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H co
góc B chung
=>ΔBAC đồng dạng với ΔBHA
b: Xét ΔBAD vuông tại A và ΔBHI vuông tạiH có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>BA/BH=BD/BI
=>BA*BI=BD*BH
c: góc AID=góc BIH=90 độ-góc HBI
góc ADI=90 độ-góc ABD
mà góc HBI=góc ABD
nên góc AID=góc ADI
=>ΔADI cân tại A
d: \(AH=\sqrt{4\cdot9}=6\left(cm\right)\)