Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: vecto AB=(1;-1); vecto AC=(2;1); vecto BC=(1;2)
AB có VTPT là (1;1)
Phương trình AB là;
1(x-1)+1(y+1)=0
=>x+y=0
AC có VTPT là (-1;2)
PT AC là:
-1(x-1)+2(y+1)=0
=>-x+1+2y+2=0
=>-x+2y+3=0
BC có VTPT là (-2;1)
PT BC là;
-2(x-2)+1(y+2)=0
=>-2x+y+6=0
b: AH có VTPT là (1;2)
Phương trình AH là:
1(x-1)+2(y+1)=0
=>x-1+2y+2=0
=>x+2y+1=0

Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).

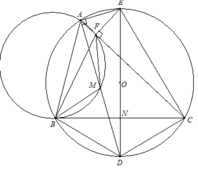
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C

a)Theo bài ra => Tam giác ABC vuông cân ở A
M(1;-1) là trung điểm BC và G\(\left(\dfrac{2}{3};0\right)\) là trọng tâm
=>\(\overrightarrow{AM}=\dfrac{2}{3}\overrightarrow{AG}\)
Giả sử A có tọa độ (a;b)
=>\(\left\{{}\begin{matrix}1-a=\dfrac{2}{3}\left(\dfrac{2}{3}-a\right)\\-1-b=-\dfrac{2}{3}b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}\\b=-3\end{matrix}\right.\)\(\Rightarrow A\left(\dfrac{5}{3};-3\right)\)
b)Do tam giác ABC vuông cân ở A=>GM vuông góc với BC
Ta có: \(\overrightarrow{GM}=\left(\dfrac{1}{3};-1\right)\)=>VTPT của đường thẳng BC là: \(\overrightarrow{n}=\left(1;-3\right)\) có M(1;-1) thuộc BC
=>phương trình đường thẳng BC:
1(x-1)-3(y+1)=0
hay x-3y-4=0
=> phương trình tham số của BC:\(\left\{{}\begin{matrix}x=3t+4\\y=t\end{matrix}\right.\)
=> tồn tại số thực t để B(3t+4;t) thuộc đường thẳng BC
MB=MA(do tam giác ABC vuông cân ở A,M là trung điểm BC)
=>\(\overrightarrow{MB}^2=\overrightarrow{MA}^2\)
=>(3t+3)2+(t+1)2=\(\left(\dfrac{2}{3}\right)^2+\left(-2\right)^2=\dfrac{40}{9}\)
=> \(t=-\dfrac{1}{3}\)hoặc \(t=-\dfrac{5}{3}\)
TH1: \(t=-\dfrac{1}{3}\)=>B\(\left(3;-\dfrac{1}{3}\right)\) ,do M(1;-1) là trung điểm BC=>C\(\left(-1;-\dfrac{5}{3}\right)\)
TH2:\(t=-\dfrac{5}{3}\)=>B\(\left(-1;-\dfrac{5}{3}\right)\),do M(1;-1) là trung điểm BC=>C\(\left(3;-\dfrac{1}{3}\right)\)
c) Tam giác ABC vuông cân ở A=>M(1;-1) là tâm đường tròn ngoại tiếp và MA là bán kính=>R2=MA2=\(\dfrac{40}{9}\)
Phương trình đường tròn ngoại tiếp tam giác ABC:
(C): \(\left(x-1\right)^2+\left(y+1\right)^2=\dfrac{40}{9}\)

a: vecto AB=(1;-1); vecto AC=(2;1); vecto BC=(1;2)
AB có VTPT là (1;1)
Phương trình AB là;
1(x-1)+1(y+1)=0
=>x+y=0
AC có VTPT là (-1;2)
PT AC là:
-1(x-1)+2(y+1)=0
=>-x+1+2y+2=0
=>-x+2y+3=0
BC có VTPT là (-2;1)
PT BC là;
-2(x-2)+1(y+2)=0
=>-2x+y+6=0
b: AH có VTPT là (1;2)
Phương trình AH là:
1(x-1)+2(y+1)=0
=>x-1+2y+2=0
=>x+2y+1=0

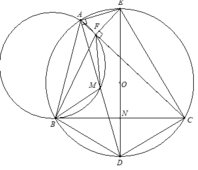
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).

Gọi (C): x^2+y^2-2ax-2by+c=0 là PT đường tròn ngoại tiêpΔACB
Theo đề, ta có:
2^2+(-1)^2-4a+2b+c=0 và 1+4+2a-4b+c=0 và 16+1+8a+2b+c=0
=>-4a+2b+c=-5 và 2a-4b+c=-5 và 8a+2b+c=-17
=>a=-1; b=-1; c=-7
=>x^2+y^2+2x+2y-7=0
=>x^2+2x+1+y^2+2y+1=9
=>(x+1)^2+(y+1)^2=9
Có \(AM=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{4^2+6^2}=\sqrt{13}\)
Do ABC là tam giác vuông nên đường tròn ngoại tiếp tam giác ABC có tâm là M
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y+2\right)^2=R^2=AM^2=13\)