Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm

a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
\(BH=\dfrac{BA^2}{BC}=\dfrac{3^2}{5}=1.8\left(cm\right)\)

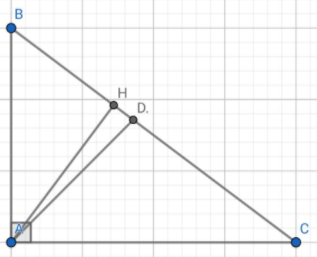
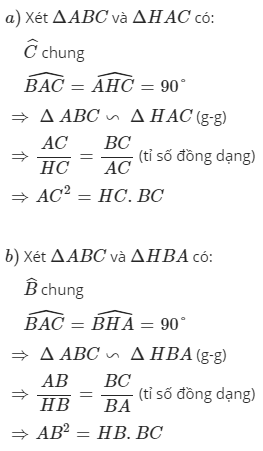

Mik copy trên mạng nên cs chút sai sót thì mog bn bỏ qua =)
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=BH\cdot BC\)

a: \(CB=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=9,6cm
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7cm; CD=80/7cm
b: Sửa đề: AB,AC
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
AM=AH^2/AB=9,6^2/12=7,68(cm)
AN=AH^2/AC=9,6^2/16=5,76(cm)
\(S_{AMHN}=7.68\cdot5.76=44.2368\left(cm^2\right)\)
Phần a dựa vào hệ thức lượng trong tam giác vuông
Phần b chứng minh tam giác đồng dạng thì sẽ ra
Phần c, d tớ chưa nghĩ ra