Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Xét tam giác $BED$ và $BAC$ có:
$\widehat{B}$ chung
$\widehat{BED}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BED\sim \triangle BAC$ (g.g)
$\Rightarrow \frac{BE}{BD}=\frac{BA}{BC}$
$\Rightarrow BE=\frac{BA.BD}{BC}=\frac{AB^2}{2BC}$
Có:
$EC^2-EB^2=(BC-EB)^2-EB^2=BC^2-2BC.EB=BC^2-2BC.\frac{AB^2}{2BC}=BC^2-AB^2=AC^2$
Ta có đpcm.

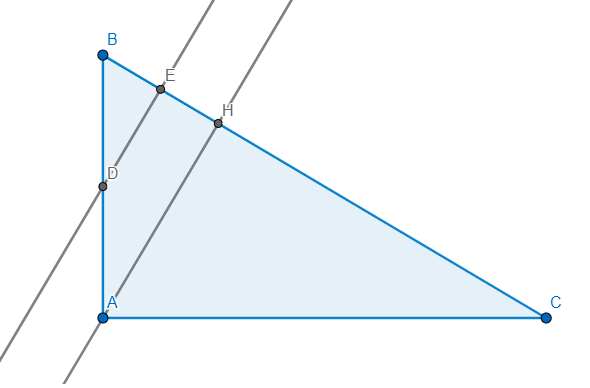
Vẽ đường cao AH \(\Rightarrow DE\parallel AH(\bot BC)\) mà D là trung điểm AB
\(\Rightarrow E\) là trung điểm BH \(\Rightarrow EB=EH\)
Ta có: \(EC^2-EB^2=\left(EC-EB\right)\left(EC+EB\right)=\left(EC-BH\right)BC\)
\(=CH.BC\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow AC^2=EC^2-EB^2\)

1/Xét tứ giác MIHC có:
góc MIC=90 độ (MI vuông góc với AC tại I)(1)
góc MHC=90 độ (MH vuông góc với BC tại H)(2)
Từ (1) và (2)=> tứ giác MIHC nội tiếp
(tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc 90 độ)
=> góc IHM=góc ICM (cùng chắn cung IM)(đpcm)
2/Tứ giác ABCM nội tiếp (O)
=> góc MCB= góc MAK (3)
Tứ giác MIHC nội tiếp (c/m trên)
=>góc MCB= góc MIK (4)
Từ (3) và (4)=> góc MAK= góc MIK
=> Tứ giác AIMK nội tiếp
(tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới 1 góc an-pha)
=>góc AKM+góc AIM=180 độ
=>góc AKM=90 độ (vì góc AIM= 90 độ)
=>MK vuông góc với BK tại K( đpcm)
Còn câu 3 và 4 đề ko có D và F nên mk ko c/m dc
chị ơi! cái này em chưa học nên chưa biết trả lời lời làm sao mong chị thông cảm

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).


Ta có : \(BD^2-CD^2=\left(MB^2-MD^2\right)-\left(MC^2-MD^2\right)=MB^2-MC^2=MB^2-MA^2=AB^2\) ( Vì MA = MB)
Vậy \(AB^2=BD^2-CD^2\)
Ta có : 2MC = AC(Vì M là trung điểm của AC)
=> 2MC.AC =AC2
Ta có ; Tam giác MDC đồng dạng tam giác BAC nên
(MC/BC) = (DC/AC)
=> MC.AC = BC.DC
=> 2.MC.AC = 2BC.Dc
=> ac2 = 2BC.DC
=> BC 2 - AC 2 = BC 2 - 2Bc - dc
=> AB2 = BC.(BC - CD - CD ) = Bc . (BD-Dc) = (BD +DC) .(BD - CD)
=> AB2 = BD2 - CD2 (ĐPCM)
Mk ko biết vẽ hình đâu nên mong bạn thứ lỗi