Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BẠN TỰ VẼ HÌNH NHA
Giải
Gọi cạnh tam giác đều ABC la a, chiều cao là h.Ta có:
a) Ta có Stam giác BMC+Stam giác CMA+Stam giác AMB =Stam giác ABC
<=>(1/2)ax+(1/2)ay+(1/2)az=(1/2)ah <=> (1/2)a.(x+y+z)=(1/2)ah
<=>x+y+z=h không phụ thuộc vào vị trí của điểm M
b) x2+y2\(\ge\)2xy ; y2+z2\(\ge\)2yz ; z2+x2\(\ge\)2zx
=>2.(x2+y2+z2) \(\ge\)2xy+2xz+2yz
=>3.(x2+y2+z2) \(\ge\)x2+y2+z2+2xy+2xz+2yz
=>x2+y2+z2 \(\ge\)(x+y+z)2/3=h2/3 không đổi
Dấu "=" xảy ra khi x=y=z
Vậy để x2 + y2 + z2 đạt giá trị nhỏ nhất thì M là giao điểm của 3 đường phân giác của tam giác ABC hay M là tâm của tam giác ABC
\(a.\)Ta có: \(S_{\Delta BMC}=\frac{BC.x}{2}\)\(\Rightarrow\)\(x=\frac{2.S_{\Delta MBC}}{BC}\)
\(S_{\Delta BMA}=\frac{BA.z}{2}\)\(\Rightarrow\)\(z=\frac{2.S_{\Delta BMA}}{AB}\)
\(S_{\Delta AMC}=\frac{AC.y}{2}\)\(\Rightarrow\)\(y=\frac{2.S_{\Delta AMC}}{AC}\)
mà \(\Delta ABC\) đều nên AB = BC = CA
suy ra \(x+y+z=\frac{2\left(S_{\Delta AMC}+S_{\Delta BMA}+S_{\Delta BMC}\right)}{AB}\)
suy ra đpcm

a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
Suy ra: AD=MN
b: Xét tứ giác AMHD có góc AMD=góc AHD=90 độ
nên AMHD là tứ giác nội tiếp
=>A,M,H,D cùng thuộc 1 đường tròn (1)
Xét tứ giác AMDN có góc AMD+góc AND=180 độ
nên AMDN là tứ giác nội tiếp
=>A,M,D,N cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,M,H,D,N cùg thuộc 1 đường tròn
=>AMHN là tứ giác nội tiếp
=>góc AHM=90 độ

a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
Suy ra: AD=MN
b: Xét tứ giác AMHD có góc AMD=góc AHD=90 độ
nên AMHD là tứ giác nội tiếp
=>A,M,H,D cùng thuộc 1 đường tròn (1)
Xét tứ giác AMDN có góc AMD+góc AND=180 độ
nên AMDN là tứ giác nội tiếp
=>A,M,D,N cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,M,H,D,N cùg thuộc 1 đường tròn
=>AMHN là tứ giác nội tiếp
=>góc AHM=90 độ

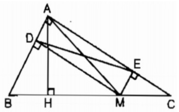
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC