Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) xét 2 tam giác BAD và tam giác BHD (góc A= góc H= 90 độ)
ta có: cạnh huyền BD chung
góc ABD= góc HBD (vì BD là phân giác góc B)
=>tam giác BAD=tam giác BHD(cạnh huyền-góc nhọn)
<=>BA=BH (2 cạnh tương ứng)
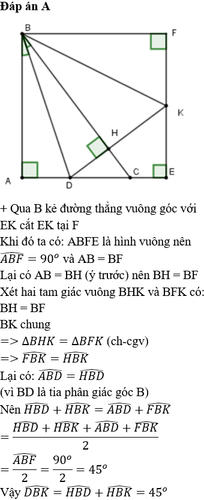
: -Kéo dài EK cắt đường thẳng vuông góc với AB kẻ từ B tại Q.
-Chứng minh được: AB=AE=BQ. Mà theo phần a), ta có: BA=BH => BH=BQ.
=> tam giác BHK= tam giác BQK( cạnh huyền- cạnh góc vuông).
=> góc HBK= góc QBK. Mà theo phần a), ta có: góc ABD= góc DBH.
=> góc DBK= 1/2.góc ABD. Mà góc ABD= 90 độ.
=> góc DBK=45 độ.(đpcm)

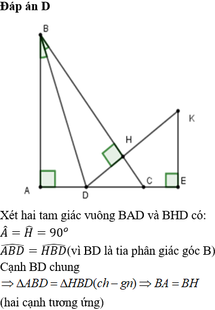
a) Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔBAD=ΔBHD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(Hai cạnh tương ứng)
Từ D kẻ \(DK\perp BC⋮H\)
Xét tam giác ABD vuông tại A và tam giác KBD vuông tại K
có: góc B1 = góc B2 (gt)
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta KBD\left(ch-gn\right)\)
=> góc D1 = góc D 2 ( 2 góc tương ứng) (1)
AD = KD ( 2 cạnh tương ứng) (*)
ta có: góc D2 + góc D3 = góc BDE
thay số: góc D2 + góc D3 = 90 độ (2)
ta có: góc D1 +( góc D2 + góc D3 )+ góc D4 = 180 độ
thay số: góc D1 +90 độ + góc D4 = 180 độ
góc D1 + góc D4 = 180 độ - 90 độ
góc D1 + góc D4 = 90 độ (3)
Từ (1);(2);(3) => góc D2 + góc D3 = góc D1 + góc D4 ( = 90 độ)
=> góc D3 = góc D4 ( góc D2 = góc D1)
Xét tam giác KDE vuông tại K và tam giác HDE vuông tại H
có: góc D3 = góc D4 (cmt)
DE là cạnh chung
\(\Rightarrow\Delta KDE=\Delta HDE\left(ch-gn\right)\)
=> KD = HD ( 2 cạnh tương ứng) (**)
Từ (*);(**) => AD = HD (=KD)
Lấy K là trung điểm BE, Tam giác ADE vuông tại D => DK=BK vậy tam giác ADK cân tại K
=> góc KBD= góc BDK
Đề bài BD là phân giác góc A =>góc BKD=góc DBA = góc BDK
=>KD//AB . Ta thấy ABHE là hình thang vuông, DK // 2 cạnh đáy và đi qua trung điểm 1 cạnh bên => DA=DH