Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì $HB:HC=1:4$ nên đặt $HB=a; HC=4a$ với $a>0$
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$14^2=a.4a$
$4a^2=196$
$a^2=49\Rightarrow a=7$ (do $a>0$)
Khi đó:
$BH=a=7$ (cm); $CH=4a=28$ (cm)
$BC=BH+CH=7+28=35$ (cm)
$AB=\sqrt{AH^2+BH^2}=\sqrt{14^2+7^2}=7\sqrt{5}$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{14^2+28^2}=14\sqrt{5}$ (cm)
Chu vi tam giác $ABC$:
$P=AB+BC+AC=7\sqrt{5}+14\sqrt{5}+35=21\sqrt{5}+35$ (cm)

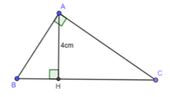
Ta có: H B H C = 1 4 ⇒ HC = 4HB
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
A H 2 = B H . C H ⇔ 4 2 = 4 B H 2 ⇔ B H = 2 ( c m ) ⇒ C H = 8 ( c m )
Ta có: BC = BH + HC = 2 + 8 = 10 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
⇒ A B 2 = B H . B C ⇔ A B 2 = 2 . 10 ⇔ A B = 20 = 2 5 ( c m )
Áp dụng định lý Pitago cho ABH vuông tại A có: A B 2 + A C 2 = B C 2
⇔ 20 + A C 2 = 100 ⇔ A C 2 = 80 ⇒ A C = 80 = 4 5 ( c m )
Vậy chu vi tam giác ABC là: 4 5 + 2 5 + 10 = 6 5 + 10 c m
Đáp án cần chọn là: D


Xét tam giác ABC vuông tại A, đường cao AH
Ta có : \(\frac{HB}{HC}=\frac{1}{4}\Rightarrow HB=\frac{1}{4}HC\)
* Áp dụng hệ thức : \(AH^2=BH.HC=\left(\frac{1}{4}HC\right)HC=\frac{1}{4}HC^2\)
\(\Rightarrow196=\frac{1}{4}HC^2\Leftrightarrow HC^2=784\Leftrightarrow HC=28\)cm
=> HB = 28/4 = 7 cm
=> BC = HB + HC = 28 + 7 = 35 cm
Áp dụng định lí Pytago tam giác AHB vuông tại H
\(AB^2=BH^2+AH^2=49+196=245\Rightarrow AB=7\sqrt{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AC=\frac{AH.BC}{AB}=14\sqrt{5}\)cm
Chu vi tam giác ABC là : \(P_{ABC}=AB+AC+BC=35+21\sqrt{5}\)cm