Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
ΔABC nội tiếp đường tròn(A,B,C∈(O))
BC là đường kính của (O)(gt)
Do đó: ΔABC vuông tại A(Định lí)
Ta có: BC=BH+HC(H nằm giữa B và C)
mà BH=9cm(gt)
và CH=16cm(gt)
nên BC=9+16=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow AB^2=9\cdot25=225\)
hay AB=15(cm)
Vậy: Khi BH=9cm và CH=16cm thì AB=15cm
b) Xét tứ giác AEMF có
\(\widehat{EAF}=90^0\)(\(\widehat{BAC}=90^0\), E∈AB, F∈AC)
\(\widehat{MFA}=90^0\)(MF⊥AC)
\(\widehat{AEM}=90^0\)(ME⊥AB)
Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
⇒MF=AE(Hai cạnh đối trong hình chữ nhật AEMF)
Ta có: EM⊥AB(gt)
AC⊥AB(gt)
Do đó: EM//AC(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
E∈AB(gt)
M∈BC(gt)
EM//AC(cmt)
Do đó: \(\dfrac{BE}{AE}=\dfrac{BM}{MC}\)(Định lí Ta lét)
⇒\(\dfrac{BE}{MF}=\dfrac{BM}{MC}\)
hay \(BE\cdot MC=BM\cdot MF\)(đpcm)
Gọi G là trung điểm của AM
Ta có: ΔAHM vuông tại M(AH⊥HM)
mà HG là đường trung tuyến ứng với cạnh huyền AM(G là trung điểm của AM)
nên \(HG=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AG=GM=\dfrac{AM}{2}\)(G là trung điểm của AM)
nên HG=AG=GM(1)
Ta có: ΔAEM vuông tại E(ME⊥AB tại E)
mà EG là đường trung tuyến ứng với cạnh huyền AM(G là trung điểm của AM)
nên \(EG=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(GA=GM=\dfrac{AM}{2}\)(G là trung điểm của AM)
nên EG=GA=GM(2)
Từ (1) và (2) suy ra GM=GA=GE=GH
hay A,E,H,M cùng thuộc một đường tròn(đpcm)

Hình bạn tự vẽ nha!!
a.)Ta có:\(AH\perp BC\Rightarrow\widehat{AHB}=90^0\)
\(BE\perp AD\Rightarrow\widehat{AEB}=90^0\)
Xét tứ giác \(AEHB\)có:
\(\widehat{AHB}=\widehat{AEB}\left(=90^0\right)\)
Mà 2 góc này cùng nhìn \(AB\)
\(\Rightarrow\)Tứ giác\(AEHB\)nội tiếp (o)
\(\Rightarrow\)\(A,E,H,B\in\)đường tròn.
b.)Có tứ giác \(AEHB\)nội tiếp
\(\Rightarrow\widehat{DEH}=\widehat{HBA}\)
\(\Rightarrow\widehat{DEH}=\widehat{CBA}\)
Trong (o) có:\(\widehat{CDA}=\widehat{CBA}\)(2 góc nội tiếp chắn cung \(AC\))
\(\Rightarrow\widehat{CDA}=\widehat{DEN}\left(=\widehat{CBA}\right)\)
Mà 2 góc này ở vị trí SLT
\(\Rightarrow EH//CD\left(\text{đ}pcm\right)\)

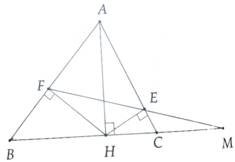
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

a: góc AEB=góc AHB=90 độ
=>AEHB nội tiếp
Xét ΔAHB vuông tại H và ΔACD vuông tại C có
góc ABH=góc ADC
=>ΔAHB đồng dạng với ΔACD
b: góc HAC+góc AHE
=góc ABE+90 độ-góc HAB
=90 độ
=>HE vuông góc AC
=>HE//CD
1)Xét tứ giác EMAF có 3 goc vg => AEMF la hcn => các điểm A,E,F,H cùng nằm trên một đường tròn
2)
dùng tứ giác nội tiếp là ra bạn à