Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BC=BD+CD=17,5\left(cm\right)\)
Áp dụng định lý phân giác:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng Pitago:
\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{3}{4}AC\right)^2+AC^2=\left(17,5\right)^2\)
\(\Leftrightarrow AC^2=196\Rightarrow AC=14\)
\(\Rightarrow AB=10,5\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=8,4\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=6,3\left(cm\right)\)
\(HD=BD-BH=1,2\left(cm\right)\)
cho tam giác abc vuông tại a, đường cao ah phân giác ad
biết bd =7,5cm; cd=10cm. Tính độ dài ah,bh,hd


Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{3}{4}\)
hay \(AB=\dfrac{3}{4}AC\)
Ta có: BD+CD=BC
nên BC=17,5cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=\dfrac{1225}{4}\)
\(\Leftrightarrow AC^2=196\)
hay AC=14cm
\(\Leftrightarrow AB=\dfrac{3}{4}AC=10.5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=8.4\left(cm\right)\\BH=6.3\left(cm\right)\end{matrix}\right.\)

Bài 1:
\(BC=CD+BD=68+51=119\)
\(AD\)là phân giác \(\widehat{BAC}\)\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\)hay \(\frac{51}{AB}=\frac{68}{AC}\)
\(\Leftrightarrow\)\(\frac{51^2}{AB^2}=\frac{68^2}{AC^2}=\frac{51^2+68^2}{AB^2+AC^2}=\frac{25}{49}\)
suy ra: \(\frac{51^2}{AB^2}=\frac{25}{49}\)\(\Rightarrow\)\(AB=71,4\)
ÁP dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Leftrightarrow\)\(BH=\frac{AB^2}{BC}=\frac{71,4^2}{119}=42,84\)
\(\Rightarrow\)\(CH=BC-BH=119-42,84=76,16\)
Bài 2:
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow\)\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow\)\(BH^2=7,5^2-6^2=20,25\)
\(\Leftrightarrow\)\(BH=4,5\)
Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}=\frac{7,5^2}{4,5}=12,5\)
\(AB.AC=BC.AH\)
\(\Rightarrow\)\(AC=\frac{BC.AH}{AB}=\frac{12,5.6}{7,5}=10\)
b) \(cosB=\frac{AC}{BC}=\frac{10}{12,5}=0.8\)
\(cosC=\frac{AB}{BC}=\frac{7,5}{12,5}=0,6\)

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{4.8^2}{3.6}=6.4\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=36\\AC^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)
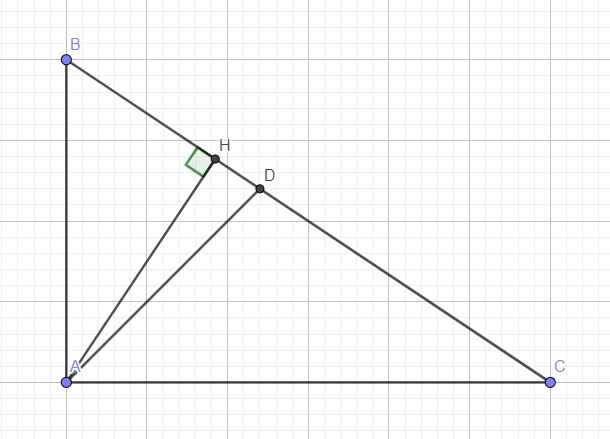
Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=7,5+10=17,5(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AB}{AC}=\dfrac{7.5}{10}=\dfrac{3}{4}\)
\(\Leftrightarrow AB=\dfrac{3}{4}AC\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=17.5^2\)
\(\Leftrightarrow AC=14\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{4}\cdot AC=\dfrac{3}{4}\cdot14=10,5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\BH\cdot BC=AB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot17.5=10.5\cdot14\\BH\cdot17.5=10.5^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AH=8,4\left(cm\right)\\BH=6,3\left(cm\right)\end{matrix}\right.\)
tính chất tia phân giác của tam giác là gì vậy bạn