Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB = \(\sqrt{881}\)
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC = \(\sqrt{\text{360,8576}}\)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ BC = ![]() = 24
= 24
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
A
C
2
=
H
C
.
B
C
⇒ AC = ![]() ≈ 20,78
≈ 20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
A
H
2
=
H
B
.
B
C
⇒ AH = ![]()

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH = 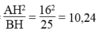
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = ![]()
≈ 29,68
A C 2 = H C . B C
⇒ AC = ![]() ≈ 18,99
≈ 18,99

a) Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (ĐL Py-ta-go)
AB2 = 152 + 252
AB2 = 225 + 625
AB2 = 850
AB = \(\sqrt{850}\)(cm)
Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA2 = BH.BC
850 = 25.BC
BC = 850:25
BC = 34
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
342 = 850 + AC2
1156 - 850 = AC2
AC2 = 306
AC = \(\sqrt{306}\)(cm)
Ta có BC = BH + HC
34 = 25 + HC
HC = 34 - 25
HC = 9
b) Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (ĐL Py-ta-go)
122 = AH2 + 62
144 = AH2 + 36
AH2 = 144 - 36
AH2 = 108
AH = \(\sqrt{108}\)(cm)
Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA2 = BH.BC
122 = 6.BC
144 = 6.BC
BC = 144:6
BC = 24 (cm)
Ta có BC = BH + HC
24 = 6 + HC
HC = 24 - 6
HC = 18
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 (ĐL Py-ta-go)
242 = 122 + AC2
AC2 = 242 - 122
AC2 = 576 - 144
AC2 = 432
AC = \(\sqrt{432}\)(cm)

a,Trong \(\Delta\) ABH có AHB=900 (BH \(\perp\) BC tại H -gt)
AH2 + BH2 =AB2 (định lý Pi-ta-go)
T/s:162 +252 =AB2
\(\Rightarrow\) AB2 =881
mà AB>0
\(\Rightarrow\) AB=\(\sqrt{881}\)\(\approx\) 29.68
Trong\(\Delta\) ABC có BAC=900 (gt), Đường cao AH (gt)
AH2= BH*CH (hệ thức lượng)
T/s: 162=25*CH
\(\Rightarrow\) CH=\(\dfrac{16^2}{25}\) = 10.24
Có:BH+HC=BC(H\(\in\) BC)
T/s: 25+10.24=BC
\(\Rightarrow\) BC=35.24
Trong \(\Delta\) ABC có:BAC=900 (GT)
AB2 +AC2 =BC2(Định lý Py-ta-go)
T/s:29.682+AC2\(\approx\)35.242
\(\Rightarrow\) AC2\(\approx\)35.242-29.682
\(\approx\)360.95
Mà AC>0
\(\Rightarrow\) AC\(\approx\) 19

a) Áp dụng Pi-ta-go cho \(\Delta AHB\)vuông tại H ta có :
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow16^2+25^2=AB^2\)
\(\Leftrightarrow AB=\sqrt{881}\left(cm\right)\)
Áp dụng hệ thức về đường cao trong tam giác vuông ta có :
\(AH^2=HB\times HC\)
\(\Leftrightarrow16^2=25\times HC\)
\(\Leftrightarrow HC=10,24\left(cm\right)\)
Ta có : \(BC=CH+BH=10,24+25=35,24\left(cm\right)\)
Áp dụng Pi-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=35,24^2-\sqrt{881}^2\)
\(\Leftrightarrow AC=360,8576\left(cm\right)\)
b) Áp dụng Pi-ta-go cho \(\Delta AHB\)vuông tại H ta có :
\(AH^2=AB^2-HB^2\)
\(\Leftrightarrow AH^2=12^2-6^2\)
\(\Leftrightarrow AH=6\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức trong tam giác ta có :
\(AH^2=CH\times HB\)
\(\Leftrightarrow CH=18\left(cm\right)\)
Ta có : \(BC=CH+BH=18+6=24\left(cm\right)\)
Áp dụng Pi-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=24^2-12^2\)
\(\Leftrightarrow AC=12\sqrt{3}\left(cm\right)\)
Vậy ...
a)
- Áp dụng định lí Py - ta - go cho tam giác vuông HAB ( \(\widehat{H}=90^o\))
\(AB^2=BH^2+AH^2\)
\(=25^2+16^2\)
\(=625+256=881\)
\(\Rightarrow AB=\sqrt{881}\approx29,6\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
+) AH2 = HB . HC
\(16^2=25.HC\)
\(HC=\frac{16^2}{25}=\frac{256}{25}=10,24\left(cm\right)\)
+) BC = BH + HC = 25 + 10,24 = 35,24 ( cm )
\(+)AC^2=HC.BC=10,24.35,24\approx360,86\left(cm\right)\)
\(\Rightarrow AC=\sqrt{360,86}\approx18,9cm\)
Vậy : ..................
b)
- Áp dụng định lí Py - ta - go cho tam giác vuông AHB ( \(\widehat{H}=90^o\)) , ta có :
AB2 = BH2 + AH2
122 = 62 + AH2
AH2 = 122 - 62
= 144 - 366 = 108 ( cm )
\(\Rightarrow AH=\sqrt{108}\approx10,39\left(cm\right)\)
- Áp dụng hệ thức lượng cho tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
\(+)AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{10,39^2}{6}=17,99\left(cm\right)\)
\(+)BC=BH+HC=6+17,99=23,99\left(cm\right)\)
\(+)AC^2=BC.HC=23,99.17,99=431,58\left(cm\right)\)
\(+)AC=\sqrt{431,58}\approx20,77\left(cm\right)\)
Vậy : ....................

Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)

Câu 2:
AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>900k^2=900
=>k=1
=>HB=25cm; HC=36cm
a. - Áp dụng hệ thức về cạnh và đường cao trong Δ vuông vào ΔABC vuông tại A ta có :
\(AH=\sqrt{CH.BH}=\sqrt{2.4}=2\sqrt{2}\) ( Đ.lý 2 )
- Áp dụng đ.lý Pytago vào \(\Delta AHB\perp H\) ta có :
\(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{2}\right)^2+4^2}=2\sqrt{6}\)
- \(BC=2+4=6\)
- Theo đ.lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}\)
b. - Áp dụng hệ thức...trong Δ vuông ABC ta có :
+ \(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=24\) ( Đ.lý 1 )
\(\Rightarrow CH=BC-BH=24-6=18\)
+ \(AH=\sqrt{BH.CH}=\sqrt{6.18}=6\sqrt{3}\) ( Đ.'ý 2 )
- Theo đ.lý Pytago ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{24^2-12^2}=12\sqrt{3}\)
a, BC = BH+HC
*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)
*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)
*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)
b,Theo định lý pytago ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)
*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)
*\(CH=BC-BH=24-6=18\)
\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)