Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)

BÀI 2 : áp dụng hệ thức lượng trong tam giác, ta có: AH^2=BH*CH=>AH^2= 4*9=36=>AH=căn bậc hai của 36=6
\(AB^2=BH\cdot BC=4\cdot\left(4+9\right)=52=>AB=\sqrt{52}=2\sqrt{13}\)
\(AC^2=CH\cdot BC=9\cdot13=117=>AC=\sqrt{117}=3\sqrt{13}\)

a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; BC = 5cm
b, AB = 15cm; AC = 20cm; AH = 12cm; BC = 25cm

Ta có:
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)
\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)
\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)
\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)

\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CH=\dfrac{AH^2}{BH}=\dfrac{36}{4,5}=8\left(cm\right)\\AB=\sqrt{4,5\left(4,5+8\right)}=\sqrt{4,5\cdot12,5}=7,5\left(cm\right)\\AC=\sqrt{8\cdot12,5}=10\left(cm\right)\end{matrix}\right.\)
và \(BC=12,5\left(cm\right)\)
\(b,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=CH\cdot BH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{AB^2}{BH}=\dfrac{36}{3}=12\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{BC^2-AB^2}{12}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2}\left(cm\right)\\AH=3\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\end{matrix}\right.\)
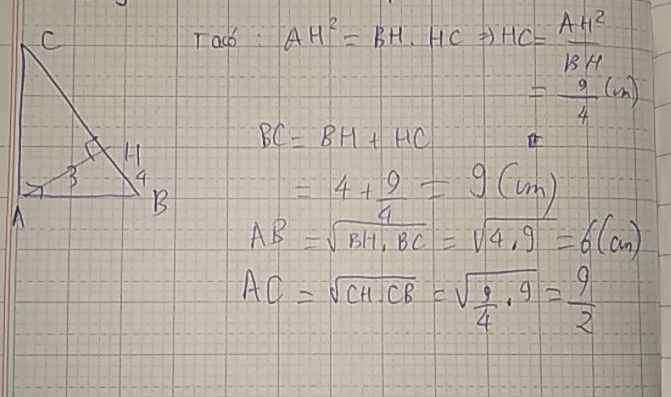
xét △ABC vuông tại A
BC2= AB2+ AC2
BC2= 32+ 42
BC2= 25
BC=\(\sqrt{25}=5\)
Xét △ABC vuông tại A, có AH là đường cao
AB.AC=AH.BC
3.4=AH.5
AH= \(\dfrac{3.4}{5}=2,4\)
Xét △ ABC vuông tại A
AB2= BH.BC
32= BH. 5
BH= 1,8
tham khảo ở đây
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-vuong-tai-a-duong-cao-ah-biet-ab-3cm-ac-4cm-tinh-do-dai-cac-canh-bc-ah-va-so-do-goc-acb-lam-tron-den-do.1482642245232
tính BH
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại ta có
AB2=BC.BH \(\Leftrightarrow\) BH=AB2/BC \(\Leftrightarrow\) BH=9/5