Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng định lý Pytago vào tam giác vuông ABC có:
AB2 + AC2 = BC2
92 + AC2 = 152
81 + AC2 = 225
AC2 = 225 - 81
AC2 = 144
AC = 12 (cm)
Xét tam giác ABC có: AB < AC < BC.
nên góc ACB < ABC < BAC ( đối diện với góc lớn hơn là cạnh lớn hơn )
b,do A là trung điểm BD (gt)
nên AB=DB
nên CA là đg trung tuyến.
Xét tam giác BCD có: CA vuông góc AB nên CA là đg cao
mà CA là đg trung tuyến.
nên tam giác BCD cân tại C
c,...

Ta có hình vẽ:
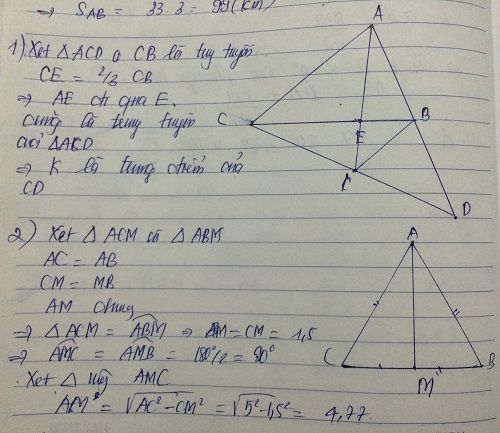
a/ Xét tam giác ABM và tam giác ACM có:
AB = AC (GT)
AM: cạnh chung
BM = MC (GT)
Vậy tam giác ABM = tam giác ACM (c.c.c)
Ta có: tam giác ABM = tam giác ACM
=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}\)+\(\widehat{AMC}\)=1800 (kề bù)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\)=900
=> AM \(\perp\)BC (đpcm)
b/ Xét tam giác BDA và tam giác EDC có:
BD = DE (GT)
\(\widehat{BDA}\)=\(\widehat{EDC}\) (đối đỉnh)
AD = DC (GT)
Vậy tam giác BDA = tam giác EDC (c.g.c)
=> \(\widehat{BAC}\)=\(\widehat{DCE}\) (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> AB // CE (đpcm)
c/ Đã vẽ và kí hiệu trên hình
d/ Xét tam giác AMB và tam giác CMF có:
AM = MF (GT)
\(\widehat{AMB}\)=\(\widehat{CMF}\) (đối đỉnh)
BM = MC (GT)
Vậy tam giác AMB = tam giác CMF (c.g.c)
=> \(\widehat{BAM}\)=\(\widehat{MFC}\) (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> AB // CF
Ta có: AB // CE (1)
Ta có: AB // CF (2)
Từ (1),(2) => EC trùng CF hay E,C,F thẳng hàng

ai giup minh cau 2a khg
chiu nay co kiem tra rui
giup minh vs![]()
![]()
![]()

a, Xét \(\Delta BAD;\Delta BED\) có:
\(\widehat{BAD}=\widehat{BED}=90^0\)
BD chung
\(\widehat{B_1}=\widehat{B_2}\) (do BD là p/g góc B)
\(\Rightarrow\Delta BAD=\Delta BED\left(CH-GN\right)\)
Vậy \(\Delta BAD=\Delta BED\)
b, Vì \(\Delta BAD=\Delta BED\)
=> AB=EB => B nằm trên trung trực của AE
AD=ED => D nằm trên trung trực của AE
=> BD là trung trực của AE.
Vậy BD là trung trực của AE.
c, Vì \(\Delta DEC\) vuông tại E => DC>DE (1)
Mà AD=ED (2)
Từ (1) và (2) => AD<DC
Vậy AD<DC
d, Ta có: \(A\in BF\) => BF=AB+AF; \(E\in BC\) => BC=EB+EC (3)
Mà AB=EB; AF=EC (4)
Từ (3) và (4) => BF=BC => tam giác BFC cân tại B => \(\widehat{BFC}=\widehat{BCF}\Rightarrow\widehat{AFC}=\widehat{ECF}\)
Xét \(\Delta AFC;\Delta ECF\) có:
AF=EC
\(\widehat{AFC}=\widehat{ECF}\)
FC chung
\(\Rightarrow\Delta AFC=\Delta ECF\left(c-g-c\right)\Rightarrow\widehat{FAC}=\widehat{CEF}\Rightarrow\widehat{CEF}=90^0\)
\(\Rightarrow FE\perp EC\). Mà \(DE\perp EC\) => FE và DE trùng nhau => E,D,F thẳng hàng
Vậy E,D,F thẳng hàng
a)
Xét \(\Delta BAD\) và \(\Delta BED\), có:
\(\widehat{BAD}=\widehat{BED}=90^0\)
BD là cạnh chung
\(\widehat{ABD}=\widehat{EBD}\) (BD là tia phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta BAD=\Delta BED\) (cạnh huyền_góc nhọn)
\(\Rightarrowđpcm\)
b)
Có: \(BA=BE\) (\(\Delta BAD=\Delta BED\))
\(\Rightarrow\) Điểm B cách đều hai điểm A và E.
\(\Rightarrow\) Điểm B thuộc đường trung trực của AE. (1)
Lại có: \(DA=DE\) (\(\Delta BAD=\Delta BED\))
\(\Rightarrow\) Điểm D cách đều hai điểm A và E.
\(\Rightarrow\) Điểm D thuộc đường trung trực của AE. (2)
Từ (1) và (2) \(\Rightarrow\) BD là đường trung trực của AE.
\(\Rightarrowđpcm\)
c)
Có: \(\widehat{DEC}=90^0\) (\(DE\perp BC\))
\(\Rightarrow DC>DE\) (Quan hệ giữa cạnh và góc đối diện trong tam giác)
Mà \(DE=DA\) (\(\Delta BAD=\Delta BED\))
\(\Leftrightarrow DC>DA\)
Hay \(AD< DC\) (đpcm)
d)
Xét \(\Delta ADF\) và \(\Delta EDC\), có:
\(\widehat{FAD}=\widehat{CED}=90^0\)
\(AF=CE\) (gt)
\(AD=DE\) (\(\Delta BAD=\Delta BED\))
\(\Rightarrow\Delta ADF=\Delta EDC\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{ADF}=\widehat{EDC}\)
Lại có:
\(\widehat{ADE}+\widehat{EDC}=180^0\) (Hai góc kề bù)
Mà: \(\Rightarrow\widehat{ADF}=\widehat{EDC}\) (chứng minh trên)
\(\Leftrightarrow\widehat{ADE}+\widehat{ADF}=180^0\)
\(\Leftrightarrow\) Ba điểm E, D, F thẳng hàng (Vì cùng nằm trên góc bẹt)
\(\Rightarrowđpcm\)
Chúc bạn học tốt!![]()

 10 K NHA !
10 K NHA !