Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

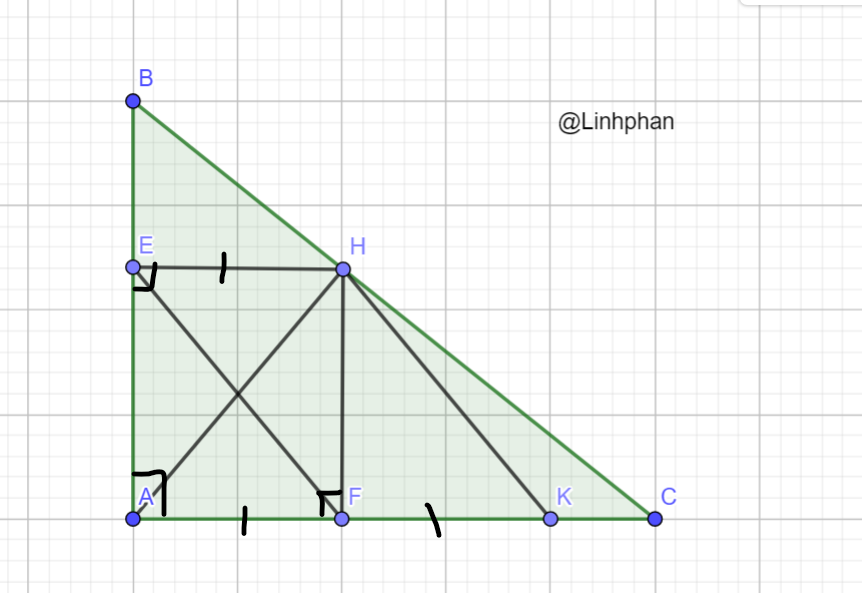
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF

a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
=>AH=EF
b: góc IFE=90 độ
=>góc IFH+góc EFH=90 độ
=>góc IFH+góc AHF=90 độ
=>góc IFH=góc IHF
=>IH=IF và góc IFC=góc ICF
=>IH=IC
=>I là trung điểm của HC
Xét ΔHAC có HO/HA=HI/HC
nên OI//AC và OI=AC/2
=>OI//AK và OI=AK
=>AOIK là hình bình hành

a/ Xét tứ giác AEHF
HE vuông góc AB; AF vuông góc AB => HE//AF
AE vuông góc AC; HF vuông góc AC => AE//HH
=> AEHF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi 1)
Mà ^BAC=90
=> AEHF là HCN => AH=EF (hai đường chéo HCN = nhau)
b/ Gọi O là giao của AH và EF
+ Xét tg vuông HCF có IH=IC => IF=IH (Trung tuyến thuộc cạnh huyền băng nửa cạnh huyền)
=> tg IHF cân tại I => ^IHF=^HFI (1)
+ Ta có AH=EF (cmt) và OA=OH; OE=OF (trong HCN các đường chéo cắt nhau tại trung điểm môic đường => OH=OF
=> tg OHF cân tại O => ^OHF=^OFH (2)
+ Mà ^IHF+^OHF=^AHC=90 (3)
=> ^HFI+^OFH=^EFI=90 => EF vuông góc với FI
