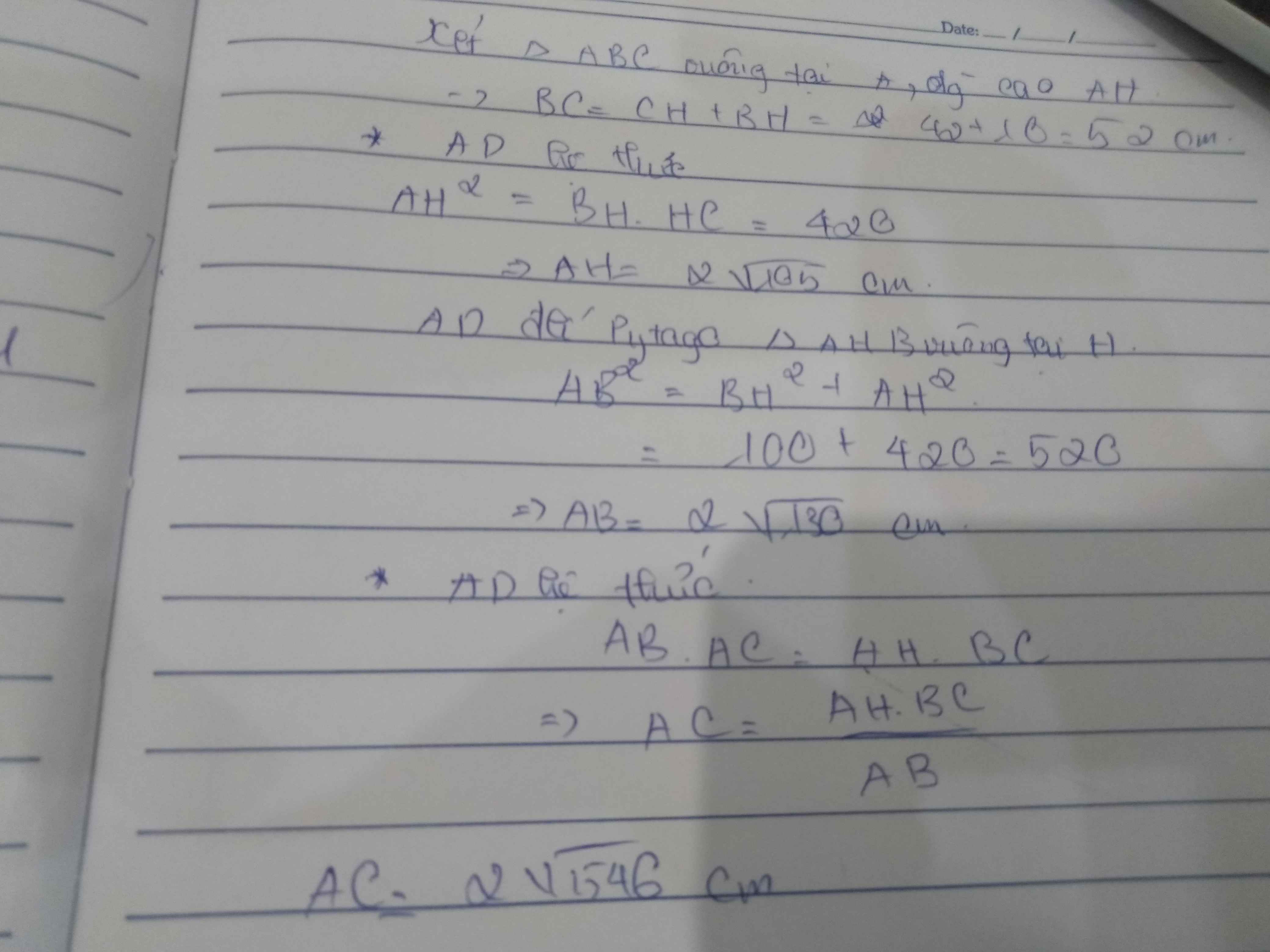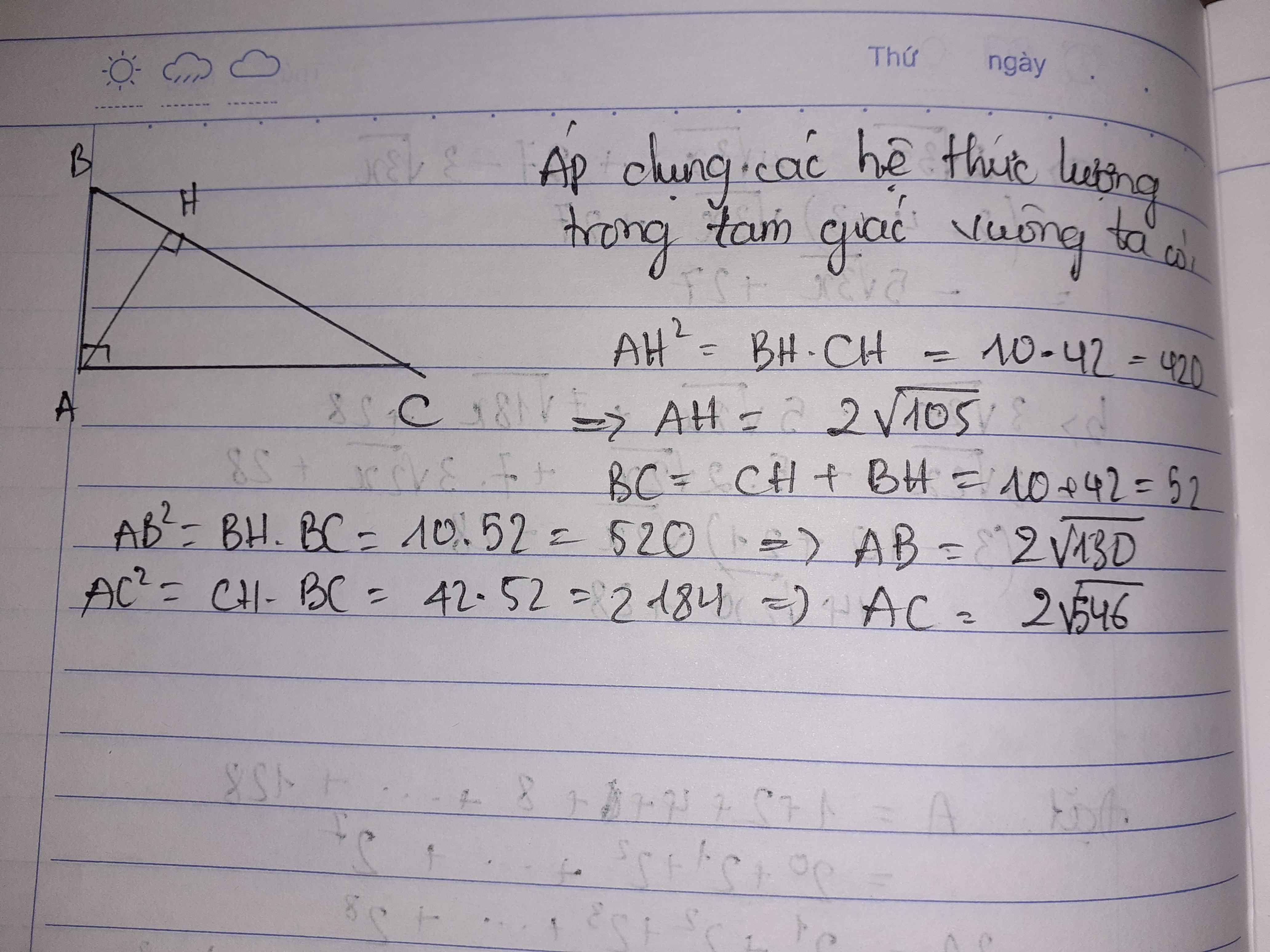Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Kẻ CH vuông góc với AB ( H thuộc AB )
Ta có : \(BH=\frac{AB-CD}{2}=\frac{30-10}{2}=10\left(cm\right)\)
Ta lại có :
\(\cos\widehat{B}=\frac{BH}{BC}\)
\(\Rightarrow BC=\frac{10}{\cos60^o}\)
Vì cos 60o = \(\frac{1}{2}\)
\(\Rightarrow BC=10.2=20\left(cm\right)\)
b) Vì ABCD là hình thang cân
M , N lần lượt là trung điểm của AB , Cd
=>MN vuông góc với CD và AB
=> MN = CH
Theo định lí py-ta-go ta có : \(CH=\sqrt{BC^2-BH^2}=\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
=> MN = \(10\sqrt{3}\)

a) Hạ đường cao CH và DK.
=> DK//CH
và DC//HK
=> DCHK là hình bình hành có \(\widehat{H}=90^o\)
=> DCHK là hình chữ nhật
=> HK=DC =10cm
Xét tam giác DAK= tam giác CBH có:
Vì\(\widehat{H}=\widehat{K}=90^o\), AD=CB ( ABCD là hình thang cân)
và \(\widehat{A}=\widehat{B}\)( ABCD là hình thang cân )
=> BH=AK =(AB-HK):2=10 cm
Xét tam giác CBH vuông tại H và có góc B bằng 60 độ
=> góc C bằng 30 độ
=> BC=2BH=20 cm
b ) N là trung điểm AB
=> N là trung điểm HK
=> MN=CH=\(\sqrt{20^2-10^2}=10\sqrt{3}\) (cm)

Cái này lên mạng search ik ,
đăng lên lại làm gì ,
có đáp án trên mạng á
a) kẻ đcao DH có tg DAH vuông tại H
AD = BC = 2AH=10.2=20cm
b) DH =MN = DAcăn3 /2 = 20.căn3/2 = 10căn3

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

Ta có: BC=BH+CH
nên BC=10+42=52cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{105}cm\\AB=2\sqrt{130}cm\\AC=2\sqrt{546}cm\end{matrix}\right.\)