Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng hệ thức lượng trong tam giác vuông, ta lần lượt có:
AI = \(\frac{AH^2}{AB}=\frac{4^2}{AB}=\frac{16}{AB}\) , \(AK=\frac{AH^2}{AC}=\frac{16}{AC}\)
Ta có SAIK = \(\frac{1}{2}AI.AK=\frac{1}{2}.\frac{16}{AB}.\frac{16}{AC}=128.\frac{1}{BC.AH}=128.\frac{1}{10.4}=3.2cm^2\)

1: BA=căn 10^2-6^2=8cm
sin ABC=AC/BC=3/5
=>góc ABC=37 độ
AH=6*8/10=4,8cm
BH=BA^2/BC=8^2/10=6,4cm
2: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
3: AI*AB=AK*AC
=>AI/AC=AK/AB
Xét ΔAIK và ΔACB có
AI/AC=AK/AB
góc IAK chung
=>ΔAIK đồng dạng với ΔACB

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HI là đường cao ứng với cạnh huyền AB, ta được:
\(AI\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC, ta được:
\(AK\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AI\cdot AB=AK\cdot AC\)
hay \(\dfrac{AI}{AC}=\dfrac{AK}{AB}\)
Xét ΔAIK vuông tại A và ΔACB vuông tại A có
\(\dfrac{AI}{AC}=\dfrac{AK}{AB}\)(cmt)
Do đó: ΔAIK\(\sim\)ΔACB(c-g-c)

a. Ta có tứ giác AIHK là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow\widehat{IKH}=\widehat{IAH}\)
Mà \(\widehat{IAH}=\widehat{KCH}\) (cùng phụ \(\widehat{ABC}\))
\(\Rightarrow\widehat{IKH}=\widehat{KCH}\)
b.
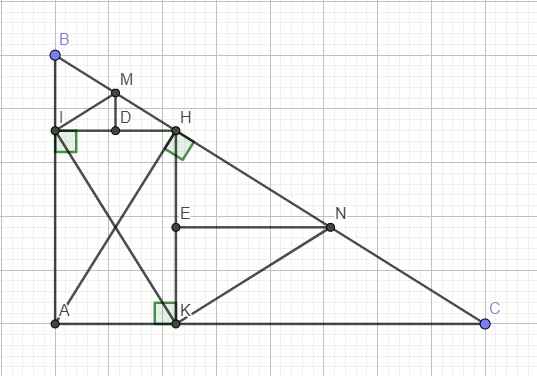
Gọi D và E lần lượt là trung điểm IH và HK
\(\Rightarrow\) MD và NE lần lượt là đường trung bình các tam giác BIH và HKC
\(\Rightarrow\left\{{}\begin{matrix}MD\perp HI\\MD=\dfrac{1}{2}BI\end{matrix}\right.\) và \(\left\{{}\begin{matrix}NE\perp HK\\NE=\dfrac{1}{2}CK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}S_{MIH}=\dfrac{1}{2}MD.IH=\dfrac{1}{2}.\dfrac{1}{2}BI.IH=\dfrac{1}{2}S_{BIH}\\S_{NHK}=\dfrac{1}{2}NE.HK=\dfrac{1}{2}.\dfrac{1}{2}CK.HK=\dfrac{1}{2}S_{HCK}\end{matrix}\right.\)
Đồng thời AIHK là hình chữ nhật \(\Rightarrow S_{IHK}=\dfrac{1}{2}S_{AIHK}\)
Do đó:
\(S_{MNKI}=S_{MIH}+S_{NHK}+S_{IHK}=\dfrac{1}{2}\left(S_{BIH}+S_{AIHK}+S_{HCK}\right)=\dfrac{1}{2}S_{ABC}\) (đpcm)

a)Áp dụng HTL2 vào tam giác ABC cuông tại A, đường cao AH ta có:
AH2=BH.HC=9.16=144
<=>AH=√144=12((cm)
Áp dụng định lý Pytago vào tam giác vuông BHA ta có:
BA2=AH2+BH2=122+92=225
<=>BA=√225=15(cm)
Áp dụng định lý Pytago vào tam giác vuông CHA ta có:
CA2=AH2+CH2=122+162=20(cm)
Vậy AB=15cm,AC=20cm,AH=12cm

a: CH=6cm
\(AB=\sqrt{BH\cdot BC}=4\left(cm\right)\)
\(\widehat{C}=30^0\)
EM CHUA HOC MOI HOC LOP 7 XIN LOI CHI TIC CHO EM CAI VOI
AI = \(\frac{8\sqrt{5}}{5}\)
AK = \(\frac{4\sqrt{5}}{5}\)
SAIK = \(\frac{8\sqrt{5}}{5}\) *\(\frac{4\sqrt{5}}{5}\) / 2 = 3,2 cm2