Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{30^2+40^2}=50$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{30.40}{50}=24$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{30^2-24^2}=18$ (cm)
b)
Theo tính chất tia phân giác:
$\frac{AD}{DC}=\frac{AB}{BC}=\frac{30}{50}=\frac{3}{5}$
$\Rightarrow \frac{AD}{AC}=\frac{3}{8}$
$\Leftrightarrow \frac{AD}{40}=\frac{3}{8}$
$\Rightarrow AD=15$ (cm)
$DC=AC-AD=40-15=25$ (cm)

Áp dụng định lí Pytago vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10cm
Do M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra:
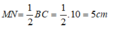
Chọn đáp án C

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)
\(\Leftrightarrow MN=\dfrac{12}{2}=6\left(cm\right)\)
b: Ta có: MN//AC và \(MN=\dfrac{AC}{2}\)
mà P\(\in\)AC và \(AP=\dfrac{AC}{2}\)(P là trung điểm của AC
nên MN//AP và MN=AP
Xét ΔABC có
M là trung điểm của AB
P là trung điểm của AC
Do đó: MP là đường trung bình của ΔABC
Suy ra: MP//BC và \(MP=\dfrac{BC}{2}\)
mà N\(\in\)BC và \(BM=\dfrac{BC}{2}\)
nên MP//BN và MP=BN
Xét tứ giác AMNP có
MN//AP
MN=AP
Do đó: AMNP là hình bình hành
Xét tứ giác BMPN có
MP//BN
MP=BN
Do đó: BMPN là hình bình hành
c) Hình bình hành AMNP trở thành hình vuông khi \(\left\{{}\begin{matrix}\widehat{MAP}=90^0\\AM=AP\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{BAC}=90^0\\AB=AC\end{matrix}\right.\)

\(a,\) \(\left\{{}\begin{matrix}AM=MB\\BN=NC\end{matrix}\right.\Rightarrow\) MN là đường trung bình tam giác ABC
\(\Rightarrow MN//AC\Rightarrow MN\perp AB\left(AC\perp AB\right)\)
\(b,MN=\dfrac{1}{2}AC\left(tính.chất.đtb\right)\)
Mà \(AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-12^2}=5\left(cm\right)\left(pytago\right)\)
\(\Rightarrow MN=\dfrac{5}{2}\left(cm\right)\)
\(c,\left\{{}\begin{matrix}AM=MB\\AP=PC\end{matrix}\right.\Rightarrow\) MP là đường trung bình tam giác ABC
\(\Rightarrow MP=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\)
\(\left\{{}\begin{matrix}AP=PC\\BN=NC\end{matrix}\right.\Rightarrow\) NP là đường trung bình tam giác ABC
\(\Rightarrow NP=\dfrac{1}{2}AB=6\left(cm\right)\)
a: Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)
hay MN\(\perp\)AB
b: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=5(cm)
\(\Leftrightarrow MN=2.5\left(cm\right)\)

Lời giải:
a) Do tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}=\frac{30.40}{2}=600$ (cm2)
b) Do $M,N$ lần lượt là trung điểm của $AB, AC$ nên:
$AM=\frac{1}{2}AB=\frac{1}{2}.30=15$ (cm)
$AN=\frac{1}{2}AC=\frac{1}{2}.40=20$ (cm)
$S_{AMN}=\frac{AM.AN}{2}=\frac{15.20}{2}=150$ (cm2)
$S_{MNCB}=S_{ABC}-S_{AMN}=600-150=450$ (cm2)
Hình vẽ: