Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AM,BN,CE lần lượt là các đường trung tuyến của ΔABC
=>AM,BN,CE đồng quy tại G
BC=căn 6^2+8^2=10cm
=>AM=5cm
=>AG=10/3cm
AN=8/2=4cm
=>BN=căn 6^2+4^2=2*căn 13(cm)
=>BG=2/3*2căn 13=4/3*căn 13(cm)
AE=6/2=3cm
CE=căn 3^2+8^2=căn 73(cm)
=>CG=2/3*căn 73(cm)

Tham khảo tại đây:
https://olm.vn/hoi-dap/detail/4163827016.html

Gọi AM là đường trung tuyến của \(\Delta ABC\) thì AM phải đi qua điểm G.
Áp dụng định lí Pitago vào \(\Delta ABC\) vuông tại A, ta có:
\(AB^2+AC^2=BC^2\)
Thay số vào, tính được BC = 13 cm
Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC nên:
\(AM=\frac{1}{2}BC=\frac{1}{2}.13=6,5\left(cm\right)\) (vì BC = 13 cm)
G là trọng tâm của \(\Delta ABC\left(gt\right)\Rightarrow GA=\frac{2}{3}AM=\frac{2}{3}.6.5=\frac{13}{3}\left(cm\right)\)
Vậy \(AM=\frac{13}{3}cm\)
Chúc bạn học tốt.
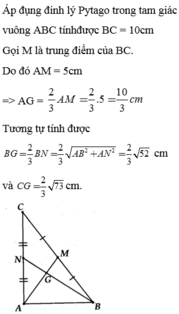
BC = \(\sqrt{3^2+4^2}\) = 5
Tam giác ABC vuông tại A => Trung tuyến AM = BC/2 = 5/2 cm
AG = 2AM/3 = 2/3 x 5/2 = 5/3 cm