Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, \(AB=\sqrt{BC^2-AC^2}=24\left(cm\right)\left(pytago\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=19,2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=10,8\left(cm\right)\\AH=\sqrt{BH\cdot CH}=14,4\left(cm\right)\end{matrix}\right.\)
a: Đề sai rồi bạn
b: BC=căn 8^2+6^2=10cm
S ABC=1/2*AB*AC=24cm2
Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng với ΔBCA
=>BA/BC=BH/BA=6/10=3/5 và S BAH/S BCA=(3/5)^2=9/25
=>DH/DA=3/5
=>HD/HA=3/8
=>S BHD=3/8*S HBA=3/8*9/25*S BCA=27/200*S BCA
Trả lời :
a, Xét \(\Delta ABC\)có :
AB2 + AC2 = 62 + 82 = 36 + 64 = 100
BC2 = 102 = 100
=> AB2 + AC2 = BC2
=> \(\Delta ABC\)vuông tại A.
Iem học ngu hình nên chỉ làm được câu a, có gì thứ lỗi -_-
a, bn dựa vào định lý Ta- lét đảo để cm nha
b, Xét \(\Delta DEC\) và \(\Delta ABC\) có
\(\widehat{EDC}=\widehat{BAC}=90^o\)
\(\widehat{BCA}\): chung
=> \(\Delta EDC\) đồng dạng vs \(\Delta ABC\left(g.g\right)\)
c, Xét tam giác ABC có AD là tia tia giác góc BAC ta đc:
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{3}{4}\)
Mà BC + CD = BC
=> BC + CD = 10
=> BD = 10 : (3+4) x 3 = 30/7 (cm)
\(S_{ABC}=\frac{6\cdot8}{2}=24\left(cm^2\right)\)
a.
Xét hai tam giác vuông HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{ABH}\text{ chung}\\\widehat{AHB}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH.BC\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=30\left(cm\right)\)
Áp dụng định lý phân giác:
\(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow\dfrac{AD}{24}=\dfrac{18-AD}{30}\)
\(\Rightarrow AD=8\left(cm\right)\)
Cho tam giác vuông góc tại A,đường cao AH, AB=15cm,BC=25cm,BH=9cm a.CM tam giác ABC đồng dạng tam giác HBA và AB.AH=BH.AC b.Phân giác của ^ABC cắt AH tại I, Tính AI và HI c.Phân giác của ^HAC cắt BC tại K. CM IK//AC (có gt kl giups em vs ạ)
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(AH=\sqrt{15^2-9^2}=12\left(cm\right)\)
BI là phân giác của góc ABH
=>IA/AB=IH/BH
=>IA/5=IH/3=(IA+IH)/(5+3)=12/8=1,5
=>IA=7,5cm; IH=4,5cm
c: góc BAK+góc CAK=90 độ
góc BKA+góc HAK=90 độ
mà góc CAK=góc HAK
nên góc BAK=góc BKA
=>BI vuông góc AK
Xet ΔBAK có
BI,AI là đường cao
=>I là trực tâm
=>IK vuông góc AB
=>IK//AC
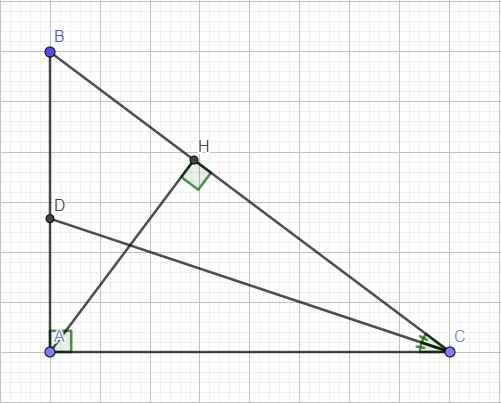
b: BH=19,2cm
AH=14,4cm