Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.

+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
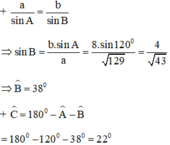

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE
+ Ĉ + B̂ = 90º ⇒ Ĉ = 90º - B̂ = 90º – 58º = 32º
+ b = a.sinB = 72 . sin 58º ≈ 61,06 cm
+ c = a . cos B = 72 . cos 58º ≈ 38,15cm
+ ha = c . sin B = 38,15 . sin 58º = 32,36 cm.