Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(\widehat{ABH}+\widehat{HAB}=90^o\)( tam giác HAB vuông tại H )
và \(\widehat{HAB}+\widehat{HAC}=90^o\left(gt\right)\)
suy ra \(\widehat{ABH}=\widehat{HAC}\)( vì cùng phụ với HAB )
b) xét \(\Delta IAH \)và \(\Delta ICE\)có
IA = IC (gt)
IH =IE (gt)
góc HIA = góc EIC ( đối đỉnh )
do đó \(\Delta IAH=\Delta ICE\left(c.g.c\right)\)
suy ra AH = EC ( 2 cạnh tương ứng )
và \(\widehat{HAI}=\widehat{ECA}\)(2 góc tương ứng )
xét \(\Delta HAC\)và \(\Delta ECA\)có
AH = EC (cmt)
góc HAI = góc ECA (cmt)
AC là cạnh chung
do đó \(\Delta HAC=\Delta ECA\left(c.g.c\right)\)
suy ra \(\widehat{AHC}=\widehat{CEA}\)(2 góc tương ứng)
mà \(\widehat{AHC}=90^o\Rightarrow\widehat{CEA}=90^o\)
hay \(CE⊥AE\)

a: \(\widehat{CDA}+\widehat{HAD}=90^0\)
\(\widehat{CAD}+\widehat{BAD}=90^0\)
mà \(\widehat{HAD}=\widehat{BAD}\)
nên \(\widehat{CDA}=\widehat{CAD}\)
b: Ta có: ΔCIH cân tại C
mà CM là đường trung tuyến
nên CM là tia phân giác của góc ICH
=>CM là tia phân giác của góc ACD
Ta có: ΔCAD cân tại C
mà CM là đường phân giác
nên CM là đường trung trực

Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)

Có gì khong hiểu hỏi lại cj nhé:
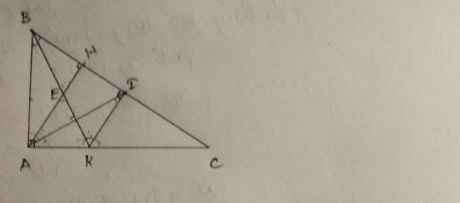
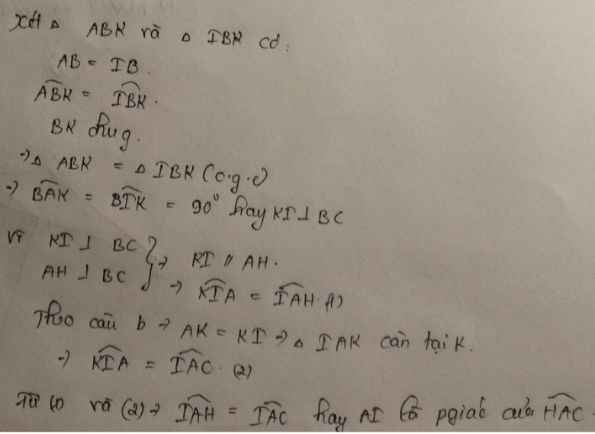
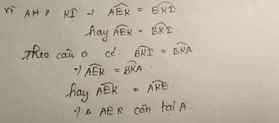
a, b ,c lần lượt từ trên xuống.