Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có AB : AC = 3 : 4 ⇔ A B 3 = A C 4 ⇒ A B 2 9 = A C 2 16
= A B 2 + A C 2 9 + 16 = A B 2 + A C 2 25 = B C 2 25 = 225 25 = 9
(Vì theo định lý Py-ta-go ta có A B 2 + A C 2 = B C 2 ⇔ A B 2 + A C 2 = 225 )
Nên A B 2 9 = 9 ⇒ AB = 9; A C 2 9 = 9 ⇒ AC = 12
Theo hệ thức lượng trong tam giác vuông ABC ta có:
A B 2 = B H . B C ⇒ B H = A B 2 B C = 81 15 = 5 , 4
Vậy BH = 5,4
Đáp án cần chọn là: A

Ta có : \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Theo định lí Pytago tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow\left(\frac{3}{4}AC\right)^2+AC^2=225\Rightarrow AC=12\)cm
\(\Rightarrow AB=\frac{3}{4}AC=\frac{3}{4}.12=9\)cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thúc : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{81}{15}=\frac{27}{5}\)cm
\(\Rightarrow CH=BC-BH=15-\frac{27}{5}=\frac{48}{5}\)cm

B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia

ta có BC=15cm và AB:AC=3:4
=>AB=9cm; AC=16cm
ta có AB2= BH.BC
=>BH= AB2/BC
<=>BH= 92/15
<=>BH=27/5(cm)
BC=BH+CH (=15cm)
=>CH= BC-BH
<=>CH=15- 27/5
<=>CH=48/5 (cm)

\(\frac{AB}{AC}\)=\(\frac{3}{4}\)\(\Rightarrow\)\(\frac{AB}{3}\)=\(\frac{AC}{4}\)
AD tinh chay day ti so bang nhau ta co : \(\frac{AB}{3}\)=\(\frac{AC}{4}\)=\(\frac{AB+AC}{3+4}\)=\(\frac{BC}{7}\)=\(\frac{15}{7}\)
\(\Rightarrow\)AB=\(\frac{45}{7}\); AC=\(\frac{60}{7}\)
Xet \(\Delta ABC\) :
\(\Rightarrow AB^{2^{ }}\)=BH.BC \(\Rightarrow BH=\frac{135}{49}\)
Vi \(H\in BC\)\(\Rightarrow BH+HC=BC\)\(\Rightarrow CH=\frac{600}{49}\)
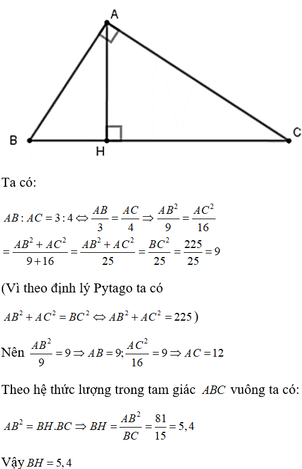
Đặt AB = 3k; AC = 4k . Áp dụng hệ thức lượng vào tam giác vuông ABC thu được k = 3. Từ đó tính được : BH = 5,4cm, HC = 9,6cm