Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

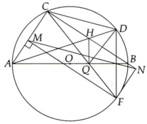
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!

Bài 1:
a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
c: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
Xét tứ giác BICD có
BI//CD(cùng vuông góc với AC)
CI//BD(cùng vuông góc với AB)
Do đó: BICD là hình bình hành
Bài 2:
a: Xét (O) có
MN=EF
OH là khoảng cách từ O đến dây MN
OK là khoảng cách từ O đến dây EF
Do đó: OH=OK
Xét ΔAHO vuông tại H và ΔAKO vuông tại K có
AO chung
OH=OK
Do đó: ΔAHO=ΔAKO
Suy ra: AH=AK
b: Xét ΔOHM vuông tại H và ΔOKE vuông tại K có
OM=OE
OH=OK
Do đó: ΔOHM=ΔOKE
Suy ra: HM=KE
Ta có: AM+MH=AH
AE+EK=AK
mà AH=AK
và HM=KE
nên AM=AE

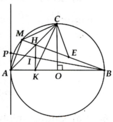
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)


a) Ta có \(IM//AE\)suy ra \(\widehat{MIH}=\widehat{EAH}\). Mà \(\widehat{EAH}=\widehat{ECH}\)nên \(\widehat{MIH}=\widehat{MCH}\). Suy ra tứ giác CIMH nội tiếp.
Dễ dàng chỉ ra được ED là tiếp tuyến của \(\left(O\right)\)suy ra \(\widehat{HED}=\widehat{HCE}\)\(\left(1\right)\)
Do tứ giác CIMH nội tiếp nên \(\widehat{CHM}=90^0\)suy ra \(\widehat{HCM}+\widehat{HMC}=90^0\)
Mà \(\widehat{HMD}+\widehat{HMC}=90^0\)nên \(\widehat{HCM}=\widehat{HMD}\)\(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)suy ra \(\widehat{HED}=\widehat{HMD}\)nên tứ giác EMHD nội tiếp. Do đó \(\widehat{HDM}=\widehat{HEM}\)mà \(\widehat{HEM}=\widehat{HCD}\)nên \(\widehat{HDM}=\widehat{HCD}\)
Từ đó chứng minh được BD là tiếp tuyến của \(\left(O_1\right)\)
b) Sử dụng tính chất đường nối tâm vuông góc với dây chung ta có: \(OO_2\perp HE,O_2O_1\perp HD\)và do \(EH\perp HD\)suy ra \(OO_2\perp O_2O_1\)
Dễ thấy \(\widehat{COM}=45^0\)suy ra \(\widehat{CAE}=45^0\)nên \(\widehat{O_2OO_1}=45^0\). \(\Delta O_2OO_1\)vuông cân tại \(O_2\)
Tứ giác OCDE là hình vuông cạnh R và \(O_2\) là trung điểm của DE nên ta tính được \(O_2O^2=\frac{5R^2}{4}\)
.Vậy diện tích \(\Delta O_2OO_1\) là\(\frac{5R^2}{8}\)

1) Dễ thấy \(\widehat{HCB}=\widehat{ACB}=90^o\)
tứ giác CBKH có \(\widehat{HKB}=\widehat{HCB}=90^o\)nên là tứ giác nội tiếp
\(\Rightarrow\widehat{HCK}=\widehat{HBK}\)( 1 )
Mà \(\widehat{ACM}=\widehat{ABM}=\frac{1}{2}sđ\widebat{AM}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{ACM}=\widehat{ACK}\)
2) Xét \(\Delta AMC\)và \(\Delta BEC\)có :
AM = BE ; AC = BC ; \(\widehat{MAC}=\widehat{CBE}=\frac{1}{2}sđ\widebat{MC}\)
\(\Rightarrow\Delta AMC=\Delta BEC\)( c.g.c )
\(\Rightarrow MC=EC\)
Ta có : \(\widehat{CMB}=\frac{1}{2}sđ\widebat{BC}=45^o\)
Suy ra \(\Delta ECM\)vuông cân tại C
3) Ta có : \(\frac{AP.MB}{AM}=R=OB\Rightarrow\frac{AP}{MA}=\frac{OB}{MB}\)
Xét \(\Delta APM\)và \(\Delta OBM\), ta có :
\(\frac{AP}{MA}=\frac{OB}{MB}\); \(\widehat{PAM}=\widehat{MBO}=\frac{1}{2}sđ\widebat{AM}\)
\(\Rightarrow\Delta APM\approx\Delta BOM\left(c.g.c\right)\)
\(\Rightarrow\Delta APM\)cân tại P ( vì \(\Delta BOM\)cân tại O )
\(\Rightarrow PA=PM\)
Gọi giao điểm của BM và ( d ) là F ; giao điểm của BP với HK là I
Xét tam giác vuông AMF có PA = PM nên PA = PM = PF
Theo định lí Ta-let, ta có :
\(\frac{HI}{FP}=\frac{BI}{BP}=\frac{KI}{AP}\Rightarrow HI=KI\)
vì vậy PB đi qua trung điểm của HK
Xin lỗi bạn nha ! Vì lỗi nên mình không vẽ được hình cho bạn ,có j bạn tự vẽ nha !!!
Bài giải
a) AB là tiếp tuyến tại A của ( C)
=> \(\widehat{BAF}=\widehat{AEF}\)
Xét \(\Delta ABF\)và \(\Delta EBA\)có :
\(\hept{\begin{cases}\widehat{ABE}chung\\\widehat{BAF}=\widehat{BEA}\end{cases}\Rightarrow\Delta ABF}\infty\Delta EBA\left(g-g\right)\)
\(\Rightarrow\frac{AB}{BE}=\frac{BF}{AB}\Rightarrow AB^2=BE.BF\)
Xét \(\Delta ABC\) vuông tại A có đường cao AH .
=> AB2 =BH . BC
=> BH . BC = BE . BF ( =AB2 )
Xét \(\Delta BHF\)và \(\Delta BEC\)có :
\(\frac{BH}{BE}=\frac{BF}{BC}\)
\(\widehat{CBE}\)chung
=> \(\Delta BHF\infty\Delta BEC\left(c-g-c\right)\)
=> \(\widehat{BHF}=\widehat{BEC}\)
*) \(\widehat{BHF}+\widehat{FHC}=\widehat{BEC}+\widehat{FHC}\)
\(\Leftrightarrow\widehat{FEC}+\widehat{FHC}=\widehat{BHC}=180^O\)
=> EFHC là tứ giác nội tiếp ( có tổng 2 góc đối =180 o
b) EFHC là tứ giác nội tiếp
=> \(\widehat{EHC}=\widehat{EFC}\)( cùng chắn góc EC )
\(\widehat{FEC}=\widehat{BHF}\)( c/ m cân A )
Mà \(\widehat{FEC}=\widehat{EFC}\)( \(\Delta ECF\)cân ở C )
=> \(\widehat{EHC}=\widehat{BHF}\)
=> 90O \(-\widehat{EHC}=90^O-\widehat{BHF}\)
<=> \(\widehat{EHD}=\widehat{FHD}\)
=> HD là phân giác góc EHF
Bạn giải câu c dùm mình được không?